머신러닝에서 대표적인 차원 축소 알고리즘은 PCA , LDA , SVD, NMF가 있습니다.
차원 축소란 매우 많은 피처로 구성된 다차원 데이터 세트의 차원을 축소해 새로운 차원의 데이터 세트를 생성하는 것입니다.
이번 포스팅에서는 PCA 분석의 개론에 대해서 최대한 자세히 내용을 담았고
다음 포스팅에서는 실제 파이썬코드와 사이킷런을 활용하여 예제 데이터를 분석합니다.
일반적으로 차원이 증가할수록 데이터 포인트 간의 거리가 기하급수적으로 멀어지게 됩니다.
차원이 증가한다는 것은 변수의 증가와 동일하다고 이해하면 되겠습니다.
( ex. iris 데이터를 예로 글면 4개의 독립변인들이 하나의 공간에 표현되기 위해서는 그 공간이 4차원이어야 합니다 )
차원이 증가할수록 희소(sparse)한 구조를 가지게 됩니다.
수백 개 이상의 피처로 구성된 데이터 세트의 경우 개별 피처간에 상관관계가 높을 가능성이 큽니다.
선형 회귀와 같은 선형 모델에서는 입력 변수 간의 상관관계가 높을 경우 이로 인한 다중 공선성 문제로 모델의 예측 성능이 감소하게 됩니다.
⭐️ 다중공선성 : 수리적으로는 어떤 독립 변수가 다른 독립 변수들과 완벽한 선형 독립이 아닌 경우를 뜻합니다. 즉 회귀 분석에서 사용된 모형의 일부 설명 변수가 다른 설명 변수와 상관 정도가 높아, 데이터 분석 시 부정적인 영향을 미치는 현상입니다.
조금 더 구체적으로 설명하자면 일반적으로 회귀 분석에서 설명 변수들은 모두 독립이라는 가정을 합니다. 설명 변수들이 모두 독립적( 서로 영향을 미치지 않음 )이어야 알아보고자 하는 변수의 영향력을 오롯이 알 수 있기 때문입니다.
만약 어느 두 설명 변수가 서로에게 영향을 주고 있다면 둘 중 하나의 영향력을 검증할 때 다른 하나의 영향력을 완벽히 통제할 수 없게되죠.
이런 문제들을 해결하기 위해서 매우 많은 다차원의 피처를 차원 축소해 피처의 수를 줄여 더 직관적으로 데이터를 해석할 수 있도록 해야합니다. 일반적으로 차원 축소는 피처 선택(feature selection) 과 피처 추출(feature extraction)으로 나눌 수 있습니다.
피처 선택은 데이터의 특징을 잘 나타내는 주요 피처만 선택하는 것이고, 피처 추출은 기존 피처를 저차원의 중요 피처로 압축해서 추출하는 것입니다.
예를 들어서 우리가 어떤 회사에 지원을 한다고 해봅시다.
지원자의 역량을 평가하는 다양한 요소로 학교 성적, 봉사활동, 수상 경력, 인턴 경험 등과 관련된 여러 가지 피처로 돼 있는 데이터 세트라면 이를 학업 성취도, 커뮤니케이션 능력, 문제 해결력과 같은 더 함축적인 요약 특성으로 추출할 수 있습니다.
이러한 함축적인 특성 추출은 기존 피처가 전혀 인지하기 어려웠던 잠재적인 요소( Latent Factor )를 추출하는 것을 의미합니다.
이처럼 차원 축소는 단순히 데이터를 압축하는 개념은 아닙니다.
PCA ( Principal Component Analysis ) - 주성분 분석
PCA는 가장 대표적인 차원 축소 기법입니다.
PCA는 여러 변수 간에 존재하는 상관관계를 이용해 이를 대표하는 주성분을 추출해 차원을 축소하는 기법입니다.
PCA는 가장 높은 분산을 가지는 데이터의 축을 찾아 이 축으로 차원을 축소하는데, 이것이 PCA의 주성분이 됩니다.
즉, 분산이 데이터의 특성을 가장 잘 나타내는 것으로 간주합니다.
PCA는 제일 먼저 가장 큰 데이터 변동성(Variance)을 기반으로 첫 번째 벡터 축을 생서앟고, 두 번째 축은 이 벡터 축에 직각이 되는 벡터( 직교 벡터)를 축으로 합니다. 세 번째 축은 다시 두 번째 축과 직각이 되는 벡터를 설정하는 방식으로 축을 생성합니다.
이렇게 생성된 벡터 축에 원본 데이터를 투영하면 벡터 축의 개수만큼의 차원으로 원본 데이터가 차원 축소됩니다.
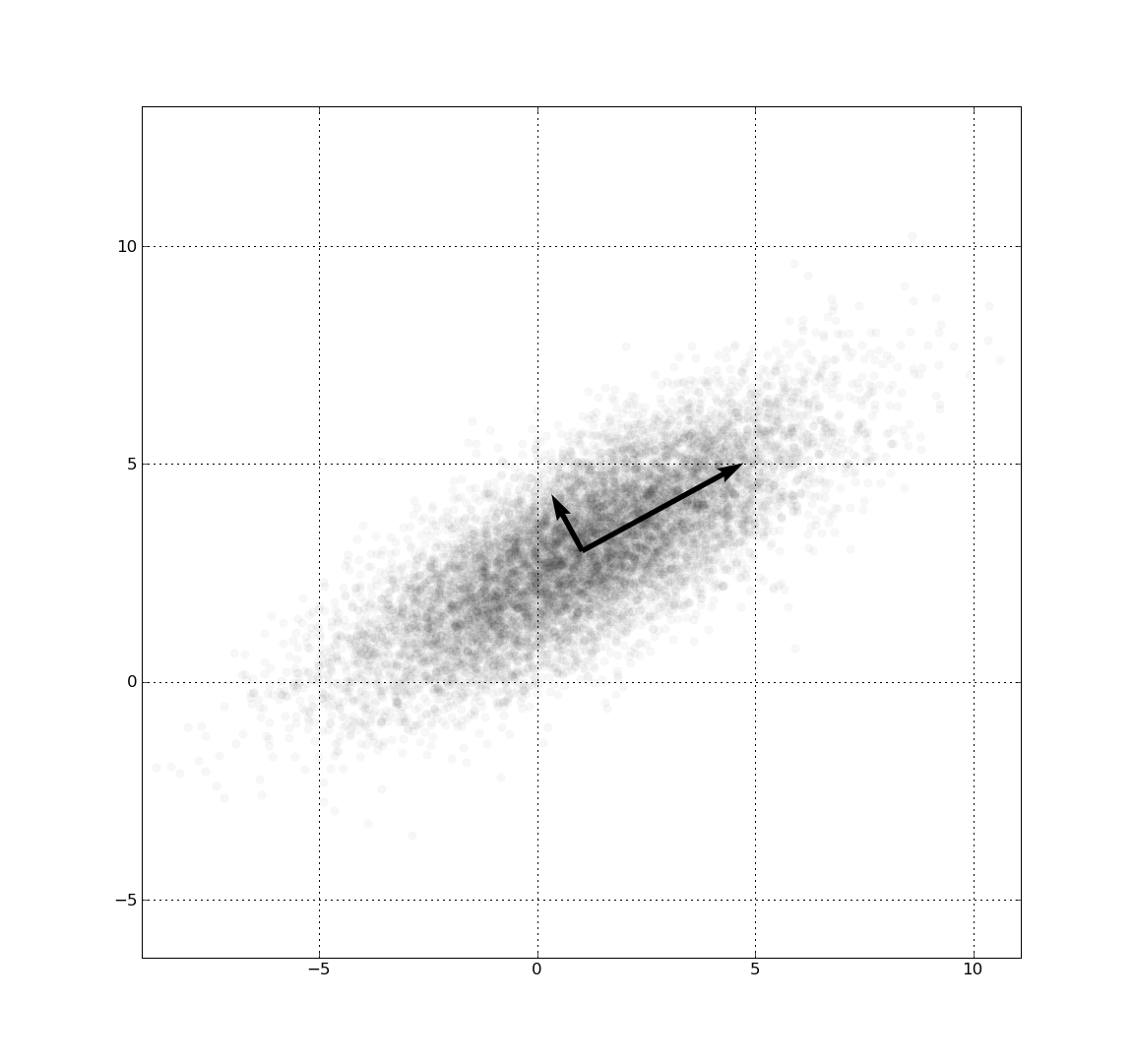
이처럼 원본 데이터의 피처 개수에 비해 매우 작은 주성분으로 원본 데이터의 총 변동성을 대부분 설명할 수 있는 분석법입니다.
선형대수 관점에서 해석해보기
PCA를 선형대수 관점에서 해석해보면 입력 데이터의 공분산 행렬 ( Convariance Matrix ) 을 고유값 분해하고
이렇게 구한 고유벡터에 입력 데이터를 선형 변환하는 것입니다.
이 고유벡터가 PCA의 주성분 벡터로서, 입력 데이터의 분산이 큰 방향을 나타냅니다.
고윳값(eigebvalue)은 바로 이 고유벡터의 크기를 나타내며, 동시에 입력 데이터의 분산을 나타냅니다.
일반적으로 선형 변환은 특정 벡터에 행렬 A를 곱해 새로운 벡터로 변환하는 것을 의미합니다.
이는 특정 벡터를 하나의 공간에서 다른 공간으로 투영하는 개념으로도 볼 수 있으며 이 경우 이 행렬을 바로 공간으로 가정하는 것입니다.
* 분산은 보통 한 개의 특정한 변수의 데이터 변동을 의미하지만, 공분산은 두 변수 간의 변동을 의미합니다.
공분산 행렬은 여러 변수와 관련된 공분산을 포함하는 정방형 행렬입니다.


다음 포스팅에서는 실제 코드를 파이썬 코드와 사이킷런으로 실습한 소스코드로 해보겠습니다 :)
