Chapter1.
머신러닝 알고리즘 마스터라는 교재로 머신러닝 복습겸 자세히 알아가기 중.
Kaggle 과 유튜브로 머신러닝을 배웠고 머신러닝의 기본적인 컨셉과 모델 사용법 등을 알고 있었고 잘 사용 중이다.
기본적인 내용 복습 겸 이 책을 선택하게 되었는데 정말 자세한 내용을 다룬다.
즉 굉장히 딥하고 어려운 내용이 많다.
특히 선형대수와 확률 및 수식이 굉장히 많기 때문에 정말 자세히 복습할 수 있다.
Capter 1 에는 굉장히 기본적인 내용들만 나오지만 처음 알게된 부분들이 많다.
머신러닝의 알고리즘을 정말 자세히 분해하여 설명하므로 머신러닝을 공부하는 사람들에게 도움이 많이 될 것 같다.
블로그에는 이 책에서 몰랐던 내용 혹은 중요하다고 생각하는 부분을 발췌해서 정리합니다.
데이터 생성 프로세스 - Data Generating Process
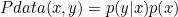
결합 확률 분포 joint probability distribution → 결합 확률 분포는 주어진 데이터로부터 확률변수 x와 y를 통해 얻은 것으로 D를 의미합니다. 즉, 결합 분포 P(x,y)는 D를 모델링하는 것입니다. 확률 변수가 반드시 두 개일 때 뿐만 아니라 확률 변수가 여러 개인 경우를 고려합니다.
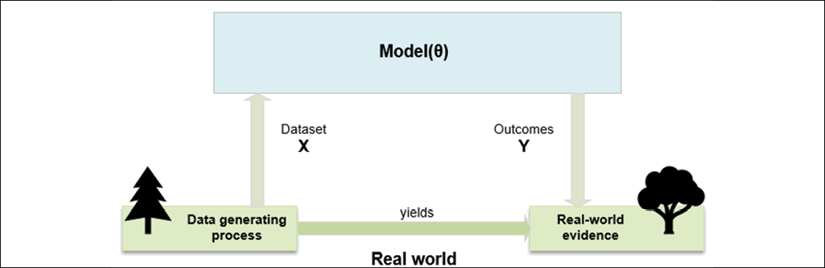
머신러닝에서 모델(model)의 정의는 벡터에 의해서 정의된 파라미터 집합에 따라 변경될 수 잇는 의사-함수(pseudo-function)로 표현되어지며, 모수(parametric) 모델과 비모수(nonparametric)모델 계열이 존재합니다.
입력 값 X에 대해서 Y를 출력시켜주는 목적 함수가 존재한다고 했을 때, 모수 학습 과정은 이 목적 함수의 정확도를 최대화( 또는 에러를 최소화)시키는 최적의 파라미터 집합을 찾는 것이다.
* 목적 함수 ( objective function ) = 손실 함수 ( loss function ) = 비용 함수 ( cost function ) : 머신러닝을 통한 예측값과 실제값의 차이(오차)와 관련한 식( equation )
** 이 함수의 값을 최소화 하거나 최대화 하는 목적의 식을 목적 함수라고 합니다.
** 예측값과 실제값의 오차를 최소화하려고 한다면 비용함수 또는 손실함수라고 합니다. 즉, 비용함수는 예측값의 오차를 최소화 하기 위해 최적화 된 식이어야 합니다.
머신러닝의 추상화( 추상성, abstraction ) -> 개별적 사례들로부터 일반적인 개념이나 원리를 형성하는 사고과정으로, 추상화는 일련의 관찰들을 요약하여 어떤 형태(패턴, 정형, 규칙 등)를 만들어내는 '일반화'와 같은 의미를 지닙니다.
'추상화'를 통해서 개념을 형성할 수 있으며, 새로운 것들을 설명하거나 예측하고, 지식을 생성할 수 있습니다.
머신러닝의 도전적인 목표는 제한된 양의 정보를 사용하여 모델을 훈련하는 최적의 전략을 찾고, 그들의 논리적인 프로세스를 정당화하는 데 필요한 모든 추상화를 찾는 것입니다.
머신러닝 작업에서 우리의 목표는 훈련 세트로 모델을 학습시키고, 검증 세트로 모델을 평가하여 최대 정확도를 달성하는 것입니다. 보다 공식적으로, 베이즈 정확도 ( Bayes accuracy )에 최대한 근접한 모델을 생성한다고 말할 수 있습니다.
도메인 적응의 목표는 특정 데이터 생성 프로세스에서 작업할 수 있는 능력을 최대화 하기 위해 모델을 M 에서 M'으로 또느 그 반대로 전환할 수 있는 최적의 방법을 찾는 것입니다.
데이터 세트 스케일링
데이터 세트에 특징별 feature-wise로 제로 평균을 가질 때 더 나은 성능을 보여줍니다. 따라서 가장 중요한 전처리 단계 중 하나는 제로-
센터링 ( zero-centering ) 으로, 모든 샘플에서 특징별 Ex[X]를 빼는 것으로 구성합니다.
** 제로-센터링을 수행한다고 해서 모든 경우에 더 나은 성능을 보여주는 것은 아닙니다. 특징에 따라서 표준 편차가 매우 다를 수 있지만 매개 변수 벡터의 크기(Norm)을 기반으로 하는 최적화는 모든 특징들을 동일한 방식으로 처리하는 경향이 있습니다. 이러한 경우에서는 결과를 도출하는 과정에서 분산이 큰 특징이 분산이 작은 특징보다 많은 영향을 미치게 됩니다.
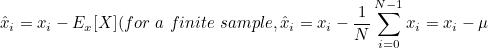
주어진 문제를 해결하는 데 분산이 큰 특징들은 상수값과 유사하게 사용됩니다.
이러한 방식에서는 변화가 적은 특징이 문제를 해결하는 과정에 영향을 미치는 능력을 잃게 되며, 이는 주로 회귀와 신경망에서 많이 발생됩니다. 이를 해결하기 위해서 제로-센터링 된 값에 각 특징별 표준 편차를 나눠주는 방법이 존재하며 이를 'z-스코어'라고 부릅니다.
아웃라이어를 가지는 데이터 세트와 같이 특정 작업에서 사용할 수 있는 스케일링 방법
* 범위 스케일링 -> 선택되어진 범위에 의해 추출된 새로운 평균과 표준 편차를 기반으로 범위를 결정합니다. [0.1] 범위에서 모든 특징들을 범위 제한하여 표준 스케일링 방법의 대안으로 사용될 수 있습니다.
* Robust 스케일링 -> 아웃라이어에 받는 영향을 최소화 하기 위해 분위수 quantiles 를 기반으로 한 Robust 접근 방법.
스케일링 수행을 위한 Scikit-Learn 클래스 사용
- StandardScaler : 기본 스케일 방법으로, 주요 매개 변수가 with_mean , with_std 둘 다 불린값을 사용하며 알고리즘이 제로-센터를 수행할지와 그것을 표준편차로 나눌지 여부를 표시함. 두 매개 변수의 디폴트 값은 True
- MinMaxScaler : 주요 매개 변수는 feature_range 로 두 개의 값 (a,b) 의 리스트 또는 튜플 형태로 값을 입력해야 하며, a<b 를 만족해야 한다. 이 매개 변수의 디폴트는 (0,1)이다.
- RobustScaler : 주로 quantile_range 매개 변수를 기반으로 하며, 이 매개변수의 디폴트 값은 IQR에 해당하는 (25,75)이다.
일반적으로 표준 스케일링을 가장 먼저 선택하며 , 범위 스케일링은 값을 특정 범위에 투영시키거나 희소성 데이터를 구성하는 데 유효하게 사용할 수 있습니다.
데이터 집합의 분석에서 아웃라이어 의 존재가 강조되고 작업이 서로 다른 분산 효과에 매우 민감할 경우에는 Robust 스케일링이 최적의 선택입니다.
정규화 Normalization
사전 정의된 Norm이 주어진 unit Norm 을 사용하여 각 벡터를 해당 벡터로 변환하는 것으로 구성합니다.
Norm 을 사용한 정규화는 각 값을 단위 반지름이 있는 초구 표면위의 점으로 변환합니다.
다른 방법과는 달리 데이터 세트를 정규화하면 기존 관계가 각거리에서만 유지되는 투영이 발생됩니다.
사이킷런 클래스에서 정규화를 수행할 수 있음.
from sklearn.preprocessing import Normalizer
nz = normalizer(norm="12")
X_nz = nz.fit_transform(X)
백색화 whitening
제로-센터링된 데이터 세트를 항등 공분산 (identity covariance) 행렬을 적용하는 연산
훈련, 검증, 테스트 세트
훈련 데이터 세트 : 모델을 학습시키는 데 사용
검증 데이터 세트 : 훈련 데이터 세트와 중복되지 않고, 편향 bias 없이 모델의 스코어를 평가하는 데 사용됩니다.
테스트 데이터 세트 : 최종적으로 검증을 수행하는 데 사용됩니다.
사이킷런으로 훈련/테스트 크기를 저장할 수 있는 함수를 사용합니다.
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X,Y,train_size =0.7,random_state=1)
- X은 독립 동일 분포 샘플로 구성된다고 가정했지만 , 연속되는 두 개의 샘플이 강한 상관관계를 가지고 있다면 훈련 성능이 감소될 수도 있다. 따라서 데이터 세트를 셔플하는 것은 샘플들 간의 상관관계를 줄이기 위한 좋은 방법이다.
- 데이터 세트를 셔플 하는 것은 샘플들 간의 상관관계를 줄이기 위해 좋은 방법이다.
- 하지만 시간적 특성을 고려해야 하는 모델을 위한 데이터 세트라면 셔플링을 사용하면 안된다.
- Numpy 와 scikit-learn을 함께 사용할 경우, 랜덤 시드를 상수값으로 설정하면 사람들이 동일한 초기 조건으로 실험을 재현할 수 있으므로 좋은 습관이다.
교차 검증
교차 검증 cross validation CV → 잘못 선택된 테스트 세트를 검출하기 위한 검증 방법.
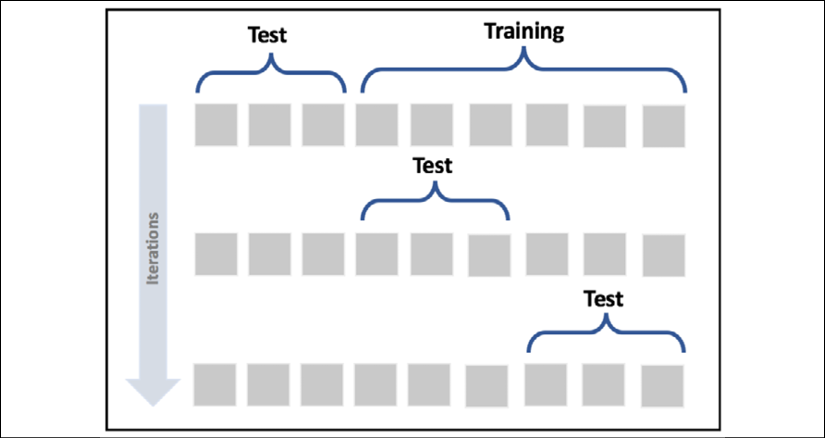
k-폴드 교차-검증 라는 방법은 전체 데이트 세트를 k개로 분할하여 서브 데이터 세트를 구성하고 , k번의 테스트 과정을 수행하게 됩니다. 즉 , 테스트가 한 번 진행될 때마다 서브 데이터 세트 중에서 하나를 테스트 세트, 나머지를 훈련 세트로 설정한다.
평균 cv 정확도는 훈련과 테스트 세트의 균형적인 크기에 의존합니다. 따라서 폴더의 수가 늘어나면 성능의 개선을 기대해야 합니다. [5,15] 범위의 값이 가장 합리적인 선택인 경우가 많습니다.

또한, 좋은 선택의 목표는 cv의 확률성을 극대화하여 추정치 사이의 교차-상관 관계를 줄이는 것입니다.
매우 작은 폴드 수는 많은 모델들이 높은 상관 관계를 갖는다는 것을 의미하지만, 지나치게 큰 폴더 수는 모델의 학습 능력을 감소시킨다. 따라서 좋은 절충은 매우 작은 값( 데이터 세트가 극히 작은 경우 제외)이나 매우 큰 값의 선택을 피해야함.
머신러닝 모델들의 특징
모델의 가용성
지도 학습된 모델을 파라미터화된 함수의 집합으로 생각한다면, 우리는 모델의 표현 가용성 representational capacity 을 상대적으로 많은 수의 데이터 분포를 매핑하는 일반적 함수의 본질적인 능력으로 정의할 수 있다.
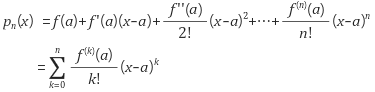
→ 미분 가능한 함수 f(x)를 이용하여 포인트 x0을 시작으로 테일러 확장합니다.
Vapnik-Chervonenkis 가용성
분류기 가용성의 수학적 공식화는 Vapnik-Chervonenkis 이론에 의해 제시되었다. 이 정의를 도입하기 위해서는 shattering에 대한 개념을 알아야 합니다.
- 만약 집합들 C와 하나의 집합 M에서 하나의 클래스를 가진다고 했을 경우, C가 M을 조각낸다 shatter라고 이야기합니다.
Vapnik-Chervonenkis 이론에 따르면 가능한 모든 레이블 할당에 대한 분류 오류가 없다면 모델 f는 X를 조각낸다고 이야기할 수 있습니다. 따라서 VC-가용성(Vapnik-Chervoniks-capacity) 또는 VC-차원(VC-dimension) 을 X 서브셋의 최대 카디널리티로 정의하여 f가 이를 분해할 수 있다.
추정량의 편향
학습 과정의 목표는 분류의 정확도를 극대화하기 위해 파라미터를 추정하는 것이다. 파라미터와 관련하여 추정량의 편향을 정의하면 다음과 같다.
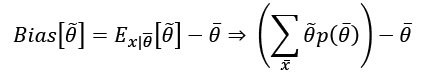
- 편향 bias 는 추정의 기댓값과 실제 파라미터 값 사이의 차이이다. 추정은 X의 함수이므로 합계에서 상수로 간주할 수 없다는 점을 기억해야 합니다.
- 추정량은 다음과 같은 경우에 편향이 없다고 합니다.

추정량이 k → 무한 일 때 추정 값의 순서가 실제 값으로 수렴하는 경우에 일관된 것으로 정의합니다.

샘플 크기가 좋은 결과를 얻는 근복적인 매개 변수, 추정량의 정확도는 편향에 반비례합니다.
즉 낮은-bias 추정량은 데이터 세트 X를 높은 정밀도 레벨로 매핑할 수 있는 반면, 높은-bias 추정량은 문제를 해결하기에 충분하지 않은 능력을 가질 가능성이 높으므로 전체 역학을 검출하는 능력이 부족하다.
샘플 크기가 무한히 커질 대 편향이 없는 것들만 획득할 수 있으므로 이 정의는 이전 정의보다 분명히 약하다고 볼 수 있습니다.
X가 Pdata 를 대표하고 추정량이 편향되지 않은 경우, 합리적인 허용 오차를 가지고 동일한 평균을 얻기를 기대해야 합니다. 이 조건은 평균적으로 추정량이 실제 주변에 분포된 결과를 산출하도록 합니다.
언더 피팅 Underfitting
편향 Bias 가 높은 모델은 훈련 세트 X에 언더피팅될 가능성이 높으며, 이는 X의 전체 구조를 학습할 수 없다는 의미입니다.
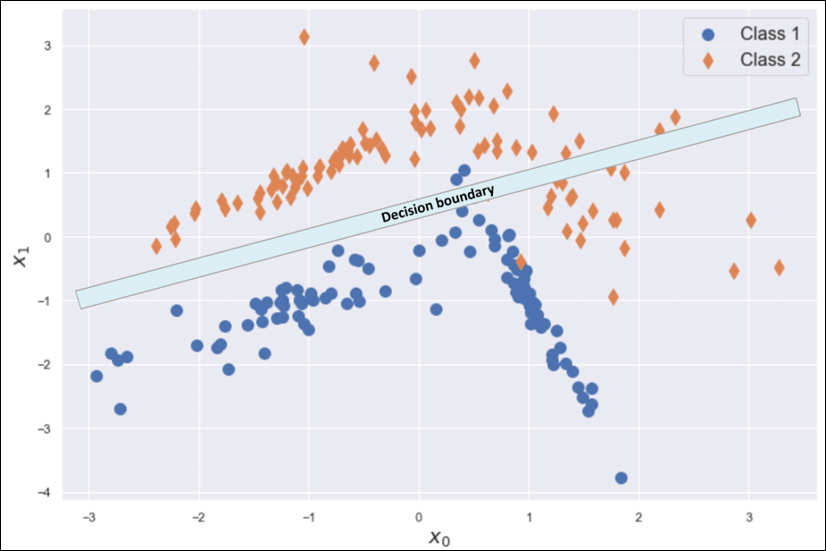
언더피팅 상태는 매우 낮은 훈련 정확도를 가집니다.
효율적인 해결책은 더 높은 가용성 모델을 채택하는 것입니다. 모수의 추정이 편향되어 있을 때 기댓값은 항상 실제값과 다릅니다.
- 이전 예에서 로지스틱 회귀와 같은 선형 모델은 분리선의 기울기와 절편만 수정할 수 있습니다. 자유도가 너무 작아서 정확도가 0.95보다 크다는 것을 쉽게알 수 있습니다.
- 이러한 문제는 선형 모델 대신 다항식 분류기를 사용하면 해결할 수 있습니다.
- 또는 다른 매개 변수인 제곱항의 계수를 도입하면 확실히 더 나은 곡선 분리선을 정의할 수 있습니다. 이때 지불해야하는 대가는 두 배입니다.
- 더 큰 가용성을 가진 모델 ( 다항식 분류기 )은 높은 계산 비용을 요구합니다.
- X가 완전하지 않은 경우, 추가 가용성으로 인해 일반화 능력이 감소할 수 있습니다.
추정량의 분산
분산은 표준 오차의 제곱으로 정의할 수 있습니다. 높은 분산은 새로운 하위 집합을 선택할 때 정확도의 극적인 변화를 암시합니다. 실제로 모델이 편향되지 않고 모수의 추정 값이 실제 평균을 중심으로 분포되어 있더라도 높은 변동성을 보일 수 있습니다.
오버피팅 Overfitting
오버피팅은 높은 분산에서 감지될 수 있는 현상입니다.
일반적으로 오버피팅이 발생하였을 경우, 매우 높은 훈련 정확도(베이즈 단계와 비슷함)를 보여주지만 검증 정확도가 좋은 것은 아닙니다. 즉, 이는 모델 가용성이 작업에 대해 충분히 높거나 심지어 과도하여( 가용성이 높을수록, 큰 분산을 가질 확률도 높음) 훈련 세트가 Pdata를 제대로 나태지 못한다는 것을 의미합니다.
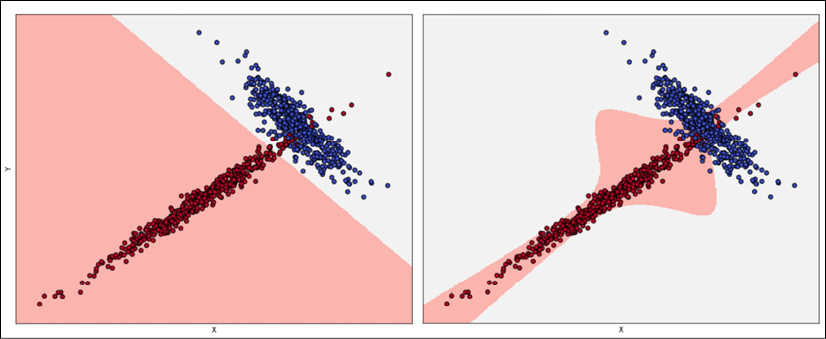
검증 정확도가 매우 낮다면 Pdata 훈련 샘플의 수를 늘리는 방법을 사용하면 좋습니다.
교차-검증은 데이터 세트의 품질을 평가하기에 좋은 방법입니다. 하지만 Pdata에 속한다고 해도 잘못 분류된 완전히 새로운 서브셋을 찾을 수도 있습니다. 훈련 세트를 확대하는 것이 불가능하다면 데이터 확장( data argumentation)은 좋은 해결책이 될 수도 있습니다.
또 다른 전략으로 규격화 regularization도 있음. ⇒ 모델 가용성을 축소와 함께 분산이 감소되는 것을 의미합니다.
