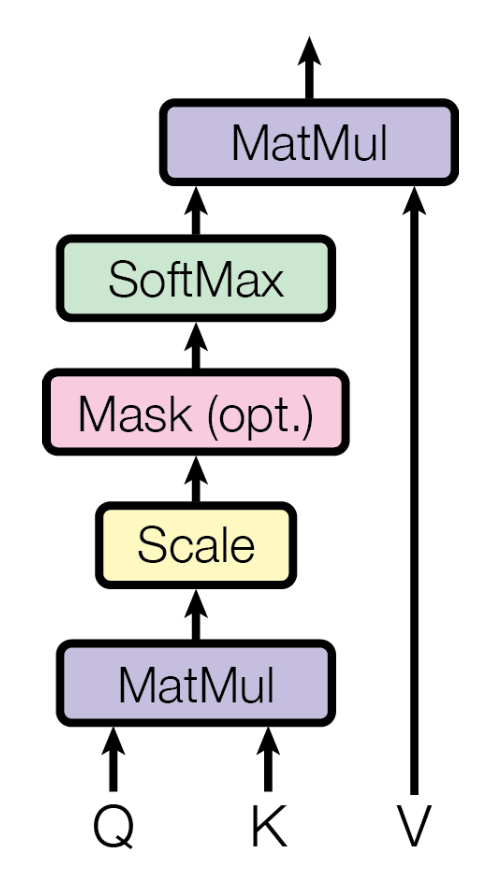
Query, Key, Value를 활용해 Attention을 계산해보자. Attention이라고 한다면 어떤 것에 대한 Attention인지 불명확하다. 구체적으로, Query에 대한 Attention이다. 이 점을 꼭 인지하고 넘어가자. 이후부터는 Query, Key, Value를 각각 Q, K, V로 축약해 부른다. Query의 Attention은 다음과 같은 수식으로 계산된다.
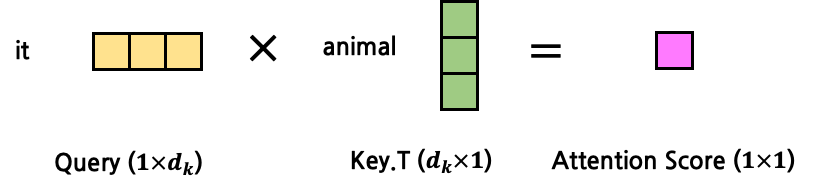
Q는 현재 시점의 token을, K와 V는 Attention을 구하고자 하는 대상 token을 의미했다. 우선은 빠른 이해를 돕기 위해 Q, K, V가 모두 구해졌다고 가정한다. 위의 예시 문장을 다시 가져와 ‘it’과 ‘animal’ 사이의 Attention을 구한다고 해보자. dk=3 이라고 한다면, 아래와 같은 모양일 것이다.

그렇다면 Q와 K를 MatMul(행렬곱)한다는 의미는 어떤 의미일까? 이 둘을 곱한다는 것은 둘의 Attention Score를 구한다는 것이다. Q와 K의 shape를 생각해보면, 둘 모두 dk를 dimension으로 갖는 vector이다. 이 둘을 곱한다고 했을 때(정확히는 K를 transpose한 뒤 곱함, 즉 두 vector의 내적), 결과값은 어떤 scalar 값이 나오게 될 것이다. 이 값을 Attention Score라고 한다. 이후 scaling을 수행하는데, 값의 크기가 너무 커지지 않도록 루트 dk로 나눠준다.
값이 너무 클 경우 gradient vanishing이 발생할 수 있기 때문이다. scaling을 제외한 연산 과정은 아래와 같다.
지금까지는 1:1 Attention을 구했다면, 이를 확장시켜 1:N Attention을 구해보자. 그 전에 Q, K, V에 대한 개념을 다시 되짚어보자. Q는 고정된 token을 가리키고, Q가 가리키는 token과 가장 높은 Attention을 갖는 token을 찾기 위해 K, V를 문장의 첫 token부터 마지막 token까지 탐색시키게 된다. 즉, Attention을 구하는 연산이 Q 1개에 대해서 수행된다고 가정했을 때, K, V는 문장의 길이 n만큼 반복되게 된다. Q vector 1개에 대해서 Attention을 계산한다고 했을 때, K와 V는 각각 n개의 vector가 되는 것이다. 이 때 Q, K, V vector의 dimension은 모두 dk 로 동일할 것이다. 위의 예시 문장을 다시 갖고 와 ‘it’에 대한 Attention을 구하고자 할 때에는 Q는 ‘it’, K, V는 문장 전체이다. K와 V를 각각 n개의 vector가 아닌 1개의 matrix로 표현한다고 하면 vector들을 concatenate해 n×dk의 matrix로 변환하면 된다. 그 결과 아래와 같은 shape가 된다.
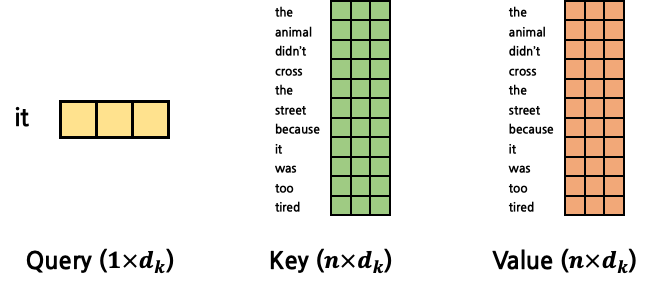
그렇다면 이들의 Attention Score는 아래와 같이 계산될 것이다.
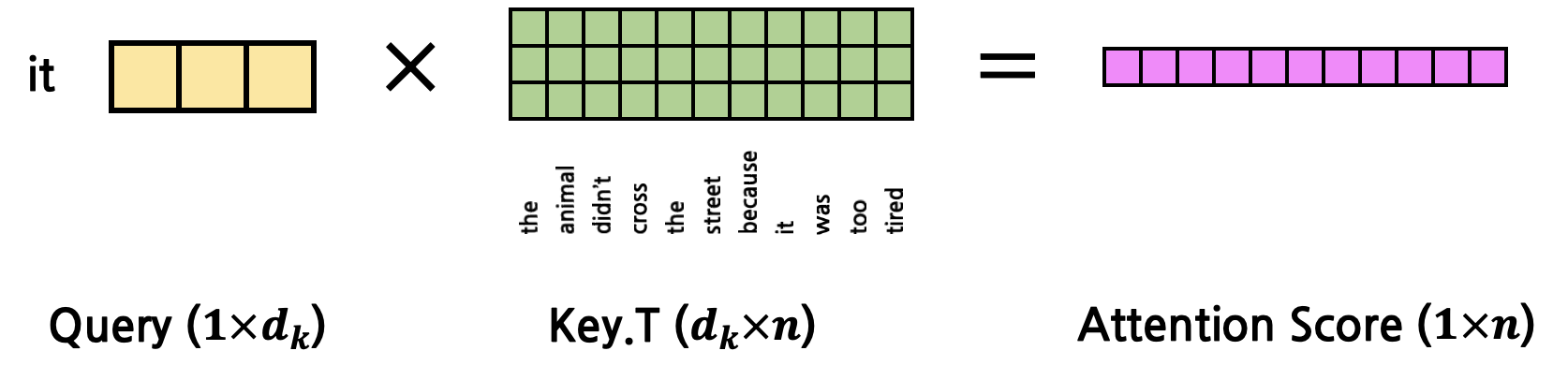
그 결과 Attention Score는 1×n의 matrix가 되는데, 이는 Q의 token과 문장 내 모든 token들 사이의 Attention Score를 각각 계산한 뒤 concatenate한 것과 동일하다. 이를 행렬곱 1회로 수행한 것이다.
이렇게 구한 Attention Score는 softmax를 사용해 확률값으로 변환하게 된다. 그 결과 각 Attention Score는 모두 더하면 1인 확률값이 된다. 이 값들의 의미는 Q의 token과 해당 token이 얼마나 Attention을 갖는지(얼마나 연관성이 짙은지)에 대한 비율(확률값)이 된다. 임의로 Attention Probability라고 부른다(논문에서 사용하는 표현은 아니고, 이해를 돕기 위해 임의로 붙인 명칭이다). 이후 Attention Probability를 최종적으로 V와 곱하게 되는데, V(Attention을 구하고자 하는 대상 token, 다시 한 번 강조하지만 K와 V는 같은 token을 의미한다.)를 각각 Attention Probability만큼만 반영하겠다는 의미이다. 연산은 다음과 같이 이루어진다.

이렇게 구해진 최종 result는 기존의 Q, K, V와 같은 dimension(dk)를 갖는 vector 1개임을 주목하자. 즉, input으로 Q vector 1개를 받았는데, 연산의 최종 output이 input과 같은 shape를 갖는 것이다. 따라서 Self-Attention 연산 역시 shape에 멱등(Idempotent)하다. (Attention을 함수라고 했을 때 syntax 측면에서 엄밀히 따지자면 input은 Q, K, V 총 3개이다. 하지만 개념 상으로는 Q에 대한 Attention을 의미하는 것이므로 semantic 측면에서 input은 Q라고 볼 수 있다.)
지금까지의 Attention 연산은 ‘it’이라는 한 token에 대한 Attention을 구한 것이다. 그러나 우리는 문장 내에서 ‘it’에 대한 Attention만 구하고자 하는 것이 아니다. 모든 token에 대한 Attention을 구해내야만 한다. 따라서 Query 역시 1개의 vector가 아닌 모든 token에 대한 matrix로 확장시켜야 한다.

그렇다면 Attention을 구하는 연산은 아래와 같이 진행된다.
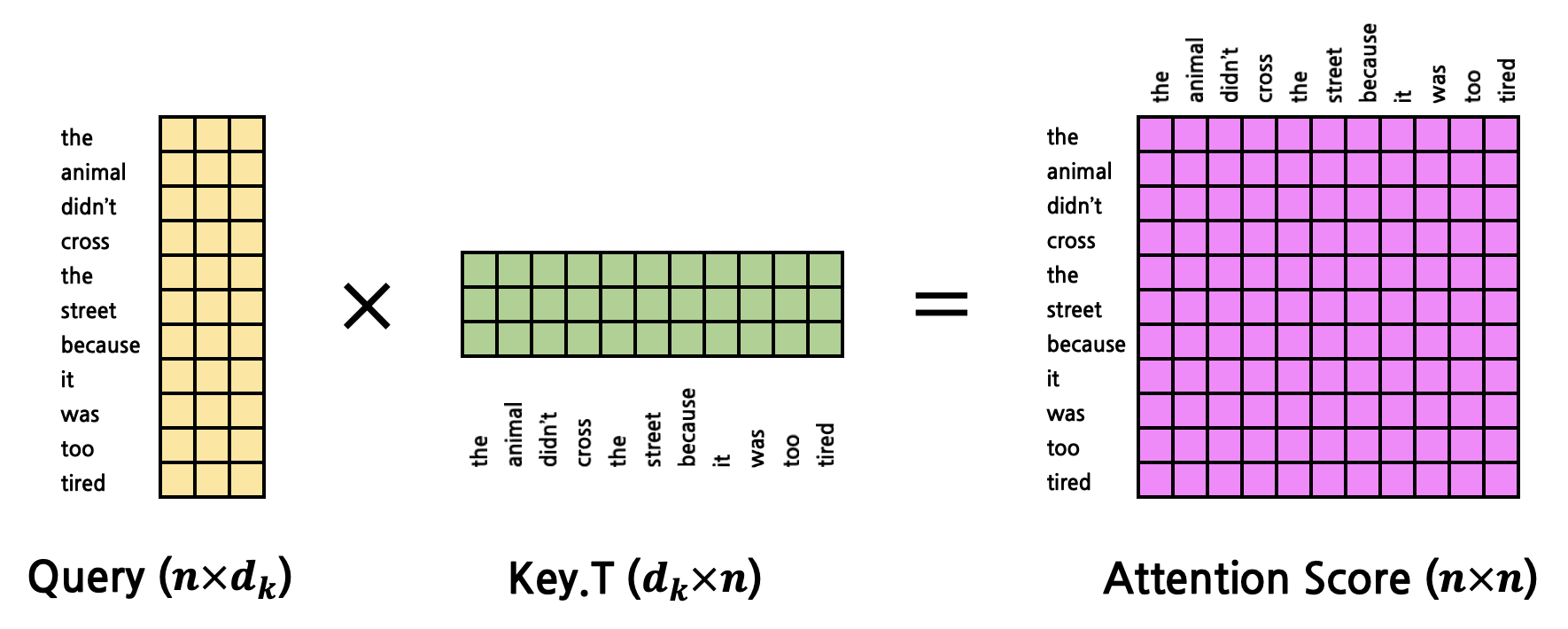

이제 여기까지 왔으면 Q, K, V가 주어졌을 때에 어떻게 Attention이 계산되는지 이해했을 것이다. 계속 반복되는 이야기이지만, Self-Attention에서 input(Q)의 shape에 대해 멱등(Idempotent)하다.

Q, K, V를 구하는 FC layer에 대해 자세히 살펴보자. Self-Attention 개념 이전에 설명했듯이, 각각 서로 다른 FC layer에 의해 구해진다. FC layer의 input은 word embedding vector들이고, output은 각각 Q, K, V이다. word embedding의 dimension이 dembed라고 한다면, input의 shape는 n×dembed이고, output의 shape는 n×dk이다. 각각의 FC layer는 서로 다른 weight matrix (dembed×dk)를 갖고 있기 때문에 output의 shape는 모두 동일할지라도 Q, K, V의 실제 값들은 모두 다르다.

