가설검정
가설과 가설 검정
모집단에 대한 새로운 주장을 대립가설 ( alternative hypothesis )이라고 하고 기존의 주장을 귀무가설(null hypothesis)이라고 합니다.
통계적 검정 ( statistical test ) 또는 가설검정 ( hypothesis test )이란 표본 데이터를 기반으로 모집단에 대한 새로운 주장의 옳고 그름을 추론하는 과정을 말합니다.
가설검정 절차
가설검정은 기본적으로 귀무가설이 사실이라는 가정 하에서 수행됩니다.
표본으로부터 검정하고자 하는 검정통계량( test statistic )을 계산합니다.
검정통계량과 그 확률분포로 부터 p-값( p-value )을 계산합니다.
- 귀무가설이 사실이라는 가정하에서 관측한 통계량과 같거나 그보다 더 극단적인 값이 발생할 확률을 의미합니다.
- 유의확률(significance probability)이라고도 합니다.
p-값이 매우 작다면 귀무가설을 기각합니다.
- 판단의 기준으로 사용하는 5% 또는 1%의 확률을 유의수준(significance level)이라고 함
- 표본으로부터 관측된 결과(즉 계산된 통계량)가 나타날 가능성이 5% 미만 또는 1% 미만이 되어 귀무가설을 기각하면 이를 통계적으로 유의하다(statistically significant)라고 표현합니다.
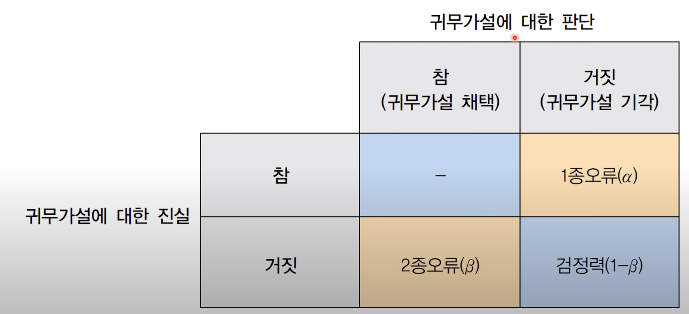
가설검정과 검정력 : 검정력이 클수록 잘못된 귀무가설을 기각할 가능성이 커집니다.
귀무가설이 참인데도 불구하고 예외적인 표본으로 인해 귀무가설을 기각 ( 대립가설 채택 ) 한다면 1종 오류라고 합니다. ( type 1 error )
반대로 귀무가설이 거짓인데도 불구하고 귀무가설을 채택한다면 2종 오류라고 합니다.
확률분포
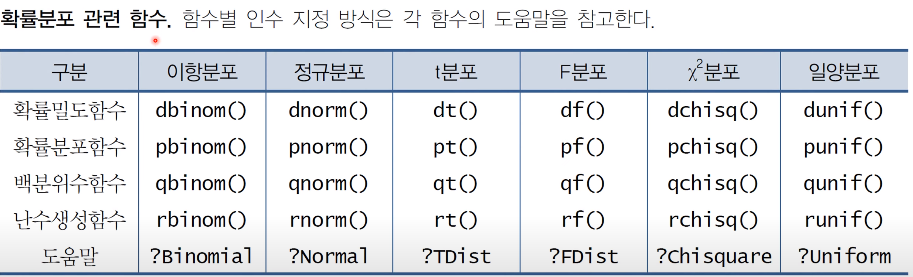
p 값을 계산하기 위해서는 검정통계량의 확률분포를 알고 있어야합니다.
각 함수 앞에 붙은 영어는 다음을 의미합니다.
d : density , p : probability, q : quantile , r : random
이항분포 ( binomial distribution )
대표적인 이산확률분포(discrete probability distribution)로서 매회 어떤 사건이 일어날 확률이 독립 시행의 경우에 있어서 이 사건이 일어나는 횟수가 만들어 내는 분포입니다.
예를 들어, 동전을 일정 횟수 반복하여 던지는 실험에서 매 시행시마다 숫자면이 나타날 확률이 1./2이라고 할 때 숫자면이 나타나는 횟수는 이항분포를 따릅니다.
R에서 동전을 10번 던졌을 때 숫자면이 7번 나오는 확률을 구해봅시다.
dbinom() 함수는 이항분포의 확률밀도함수를 뜻합니다.
함수의 첫 번째 파라미터는 사건이 발생할 횟수를 지정합니다. 위의 예시에서 숫자면이 나오는 경우가 되겠네요.
그 다음으로 시행횟수를 정하고 사건이 발생할 확률을 정해주면 됩니다.
아래의 pbinom도 같습니다.
이항분포의 확률분포함수를 구할 수 있습니다.
확률분포함수의 값은 이항분포함수의 0~7의 확률값을 합산한 것과 결과가 같습니다.


정규 분포 ( normal distribution )
대표적인 연속확률분포 ( continuous probability distribution )로서 통계적 검정을 위해 가장 널리 활용되는 분포
정규분포에서는 대부분의 관측값이 중앙에 몰려있으며 멀어질수록 그 빈도수가 점점 작아지는 종 모양의 대칭인 모습을 가집니다.

pnorm() 함수를 사용하면 정규분포의 확률분포를 구할 수 있습니다.


표준정규분포에서 표준 점수의 95% 신뢰구간을 계산할 수 있습니다.
아래의 결과를 보면 -1.95 에서 1.95 사이가 95% 신뢰구간임을 알 수 있습니다.


정규분포에서 난수를 생성하는 함수입니다.


데이터 정규성은 여러가지 방법으로 테스트할 수 있지만 Shaprio test를 이용하면 쉽게 검정할 수 있습니다.
Shaprio-wilk는 표본 데이터가 정규성을 만족한다는 귀무가설을 검증합니다.
따라서 유의수준 0.05를 적용할 때, p값이 0.05보다 커야만 귀무가설을 유지할 수 있고, 표본 데이터가 정규성을 충족한다고 결론내릴 수 있습니다.
반대로 p 값이 0.05보다 작으면 귀무가설을 기각하게 되므로 표본 데이터가 정규성을 충족한다는 주장을 유지하지 못하게됩니다.
shapiro.test(rnorm(100, mean=100, sd=10)) # 정규분포로부터 추출한 데이터 100개
shapiro.test(runif(100, min=2, max=4)) # 이량분포로부터 추출한 데이터 100개결과를 보면 정규분포로부터 추출한 데이터의 Shapiro.test 결과를 보면 p-value가 0.05보다 훨씬 큽니다.
따라서 귀무가설은 유지가 되고 정규성을 충족한다는 것을 알 수 있습니다.
반면 이량 분포로부터 추출한 데이터의 테스트 결과를 보면 p-value가 0.05에 훨씬 미치지 못하므로 귀무가설은 기각되고 정규성은 충족하지 못한다고 결론내릴 수 있습니다.

qqnorm() 함수에 표본 데이터를 인수로 제공하게 되면 R은 표준정규분포로부터 인수로 주어진 표본 데이터 크기 만큼의 이론적 표본을 추가로 생성합니다. 두 표본의 데이터를 크기 순으로 정렬하고 정렬된 각 쌍의 데이터를 산점도 형식으로 그리게 되면 정규 Q-Q 도표가 완성됩니다.
아래의 코드는 정규분포로부터 100개의 데이터를 추출해서 정규 Q-Q 도표를 생성한 것입니다.
qqnorm(rnorm(100, mean=100, sd=10),
col="blue",
main = "Simple from Normal Distribution")정규 Q-Q 도표의 x축은 이론적 정규분포로부터 생성된 표본이고, y축은 실제 표본입니다.
x축의 값은 정규분포로부터 생성된 값이기 때문에 대각선 형태로 점들이 분포한다면 정규분포를 따른다고 볼 수 있습니다.
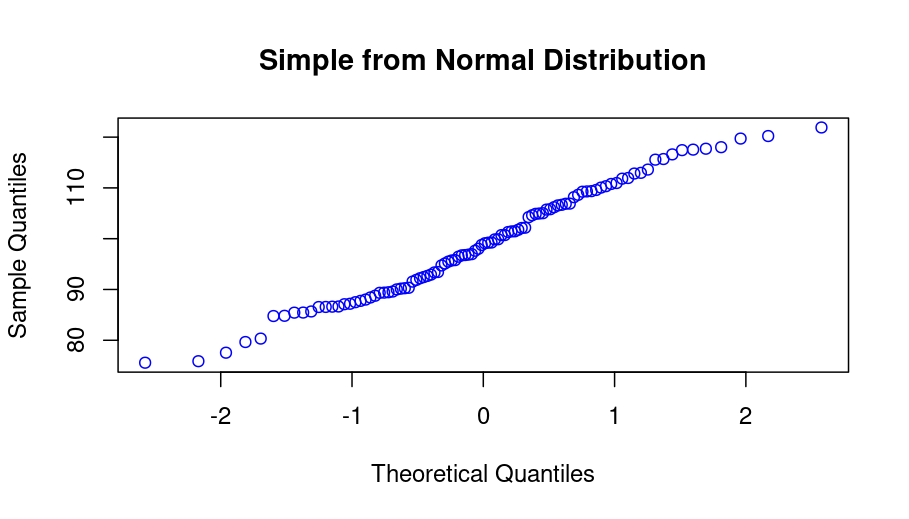
qqline() 함수를 통해 첫 번째 4분위수와 세 번째 4분위수를 통과하는 직선을 그리게 되면 정규성 충족 정도로 시각적으로 좀 더 쉽게 확인할 수 있습니다.
일양분포에 대해서도 빨간색 그래프로 그렸습니다.
일양분포로부터 추출한 표본 데이터를 그려보면 직선을 그엇을 때, 앞서 정규분포에서 추출한 데이터보다 직선이 많이 벗어나 있습니다.
이는 정규분포로부터 추출한 데이터가 정규성의 조건을 조금 더 잘 충족하고 있다는 것을 의미합니다.
qqline(rnorm(100, mean=100, sd=10))
# 위에서 확인한 일양분포
qqnorm(runif(100, min=2, max=4),
col="red",
main = "Simple from Normal Distribution")
qqline(runif(100, min=2, max=4))

