논문리뷰 - Denoising Diffusion Probabilistic Models - 노이즈를 사용했다 지웠다

https://arxiv.org/pdf/2006.11239.pdf

 

Preview

자체 Abstract

• data에 임의의 noise를 더해주는 과정을 Forward process라고 하며 noise를 제거하는 과정을 reverse process라고 한다.
• forward process (diffusion process) : data에 noise를 추가하는 과정으로, markov chain을 통해 점진적으로 noise를 더해나간다.
• reverse process : gaussian noise에서 시작하여 점진적으로 noise를 제거해가는 과정

현실의 복잡한 데이터셋을 확률분포 probability distribution으로 표현할 때 중요한 개념

• tractability: Gaussian이나 Laplace distribution 처럼 data에 쉽게 fitting되어 분석이 쉬우며 계산이 용이한 분포
• flexibility: 임의의 복잡한 data에 대해서도 적용이 가능한 분포

 

Markov Chain - 마르코프 체인 

마르코프 체인은 마르코프 성질을 가진 이산 확률과정. 마르코프 성질은 ‘특정 상태의 확률은 오직 과거의 상태에 의존한다’라는 것. 예를 들어 오늘의 날씨가 맑다면 내일의 날씨는 맑을지 비가 내릴지를 확률적으로 표현할 수 있습니다.

 

출처 - https://www.puzzledata.com/blog190423/

상태 A에서 상태 E로 전이할 확률은 0.4 반대는 0.7

상태 E와 A를 반복할 경우에는 각각 0.3과 0.6으로 보았습니다.

 

오늘 날씨에 기준하여 내일 특정 날씨가 발생할 확률

 

마르코프 체인 계산 방법

위와 같은 확률이 있을 때 우리는 아래와 같이 상태 전이도를 그릴 수 있습니다. 위의 표와 동일하게 맑음이 내일도 계속될 확률은 0.7, 맑음에서 흐림으로 갈 확률은 0.3 등으로 표현할 수 있습니다.

 

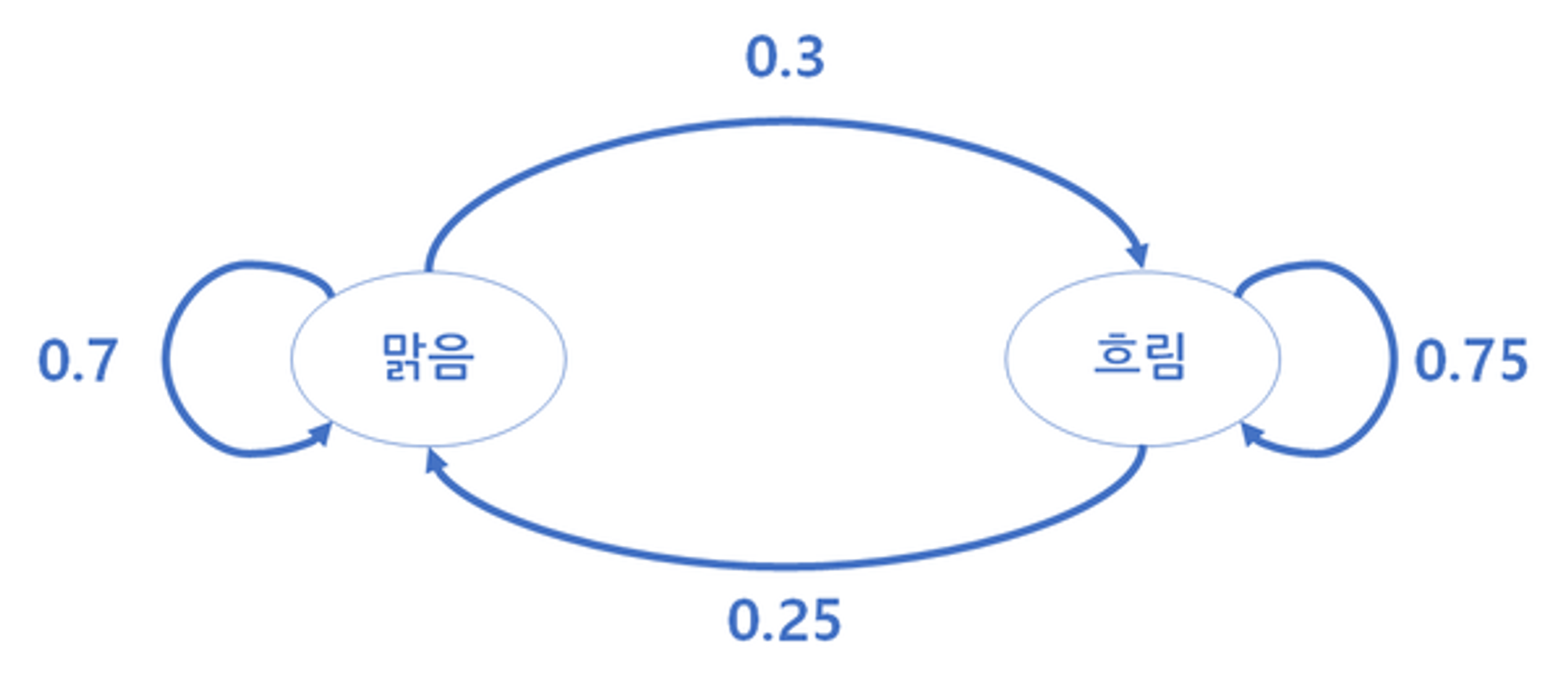
이런 전이도는 행렬로 표현할 수 있습니다.

전이행렬을 통해 모레는 날씨가 어떨지 확률 변화를 계산해보겠습니다.

 

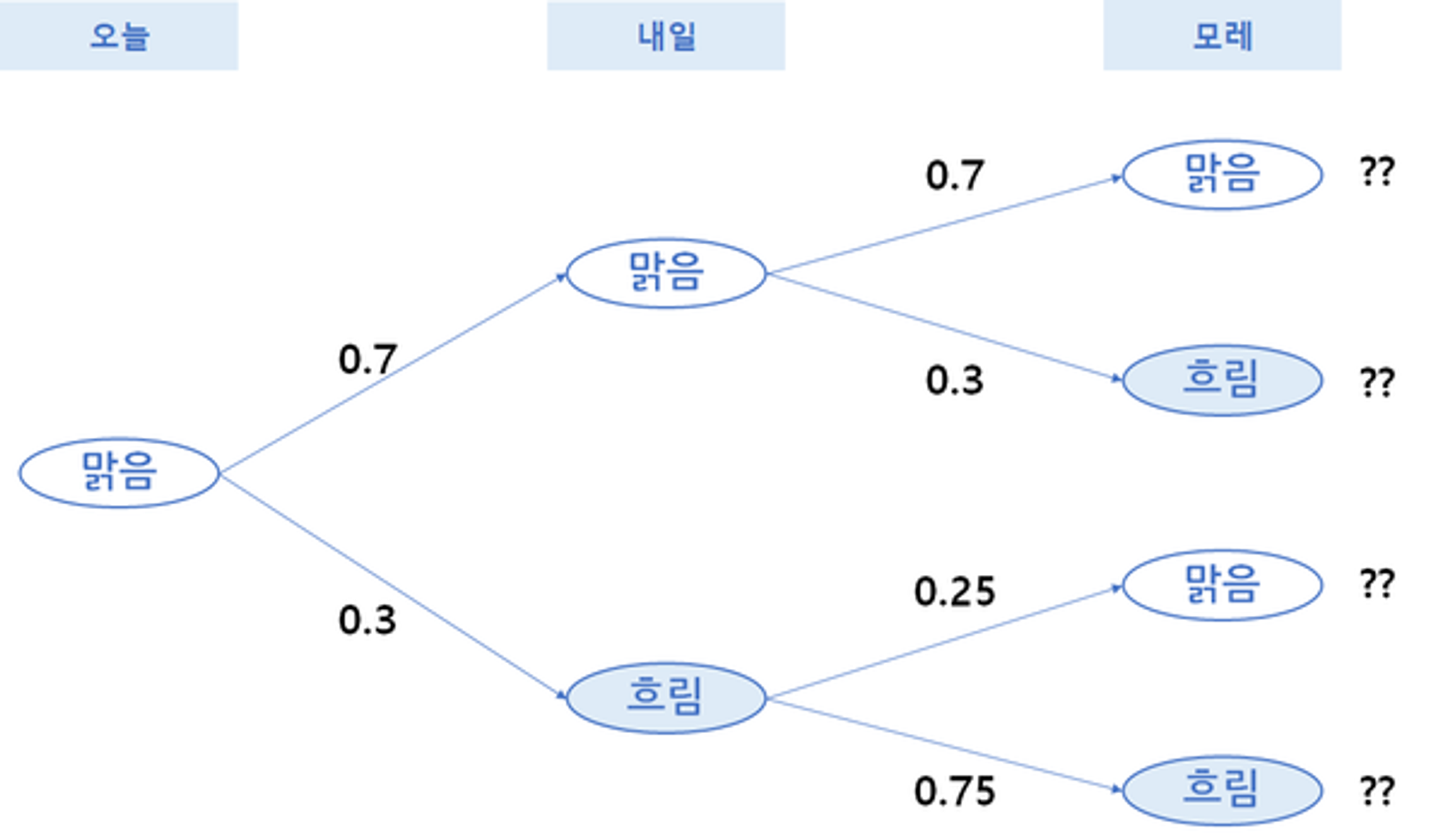
위의 전이 흐름도를 가지고 계산을 했을 때 행렬곱을 통하여 아래와 같이 계산할 수 있습니다. 다시 말해 모레의 확률 변화는 오늘과 내일의 전이가 연속되어 일어나는 경우이기 때문에 전이행렬을 곱하여 계산하게 됩니다.

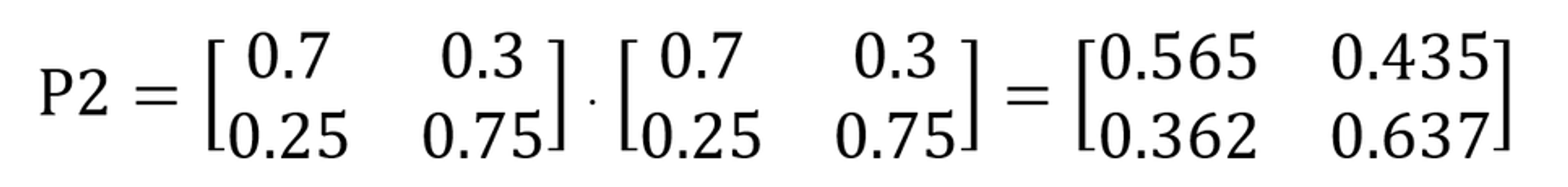
만약 지난 3년간 특정 일의 날씨 중 80%가 맑았다면 특정일 기준 모레가 맑음 확률은 0.8 x 0.565 + 0.2 x 0.362 = 0.524이기 때문에 52.4% 확률로 예측할 수 있게 됩니다.

 

이러한 상태에서 충분히 많은 횟수를 반복한다면 어느 순간에는 전이행렬이 변하지 않는 상태가 오는데 이를 두고 안정상태(steady state)라 부르고, 확률이 직전 상태와 동일하게 수렴하게 됩니다. 이러한 확률 분포를 정적분포(Stationary Distribution)라고 부르게 됩니다.

 

출처 - https://www.puzzledata.com/blog190423/

마르코프 체인에 관하여 - PuzzleData

 

Diffusion Model

 

딥러닝에서 현실의 복잡한 dataset을 확률분포 probability distribution로 표현하는 것은 매우 중요합니다.

특히 우리가 이 확률분포를 구하고자 할 때에는 tractability와 flexibility라는 개념이 중요한데, 이는 서로 trade-off 관계에 있기 때문에 이 둘을 동시에 만족하긴 어렵습니다. (복잡한 data에 대해서도 잘 fitting이 되어 있으면서도 계산이 용이한 분포를 찾긴 어려움)

 

다른 생성 모델들과 비교했을 때 복잡한 구조를 가지는 GAN 혹은 VAE와 다르게 Diffusion model은 이미지를 encoding 하는 forward process를 유지하며 image를 decoding하는 reverse process - Single network만을 학습합니다. 

 

2.1 Forward Process ( diffusion process )

markov chain으로 data에 점진적으로 noise를 추가하는 과정입니다.

 

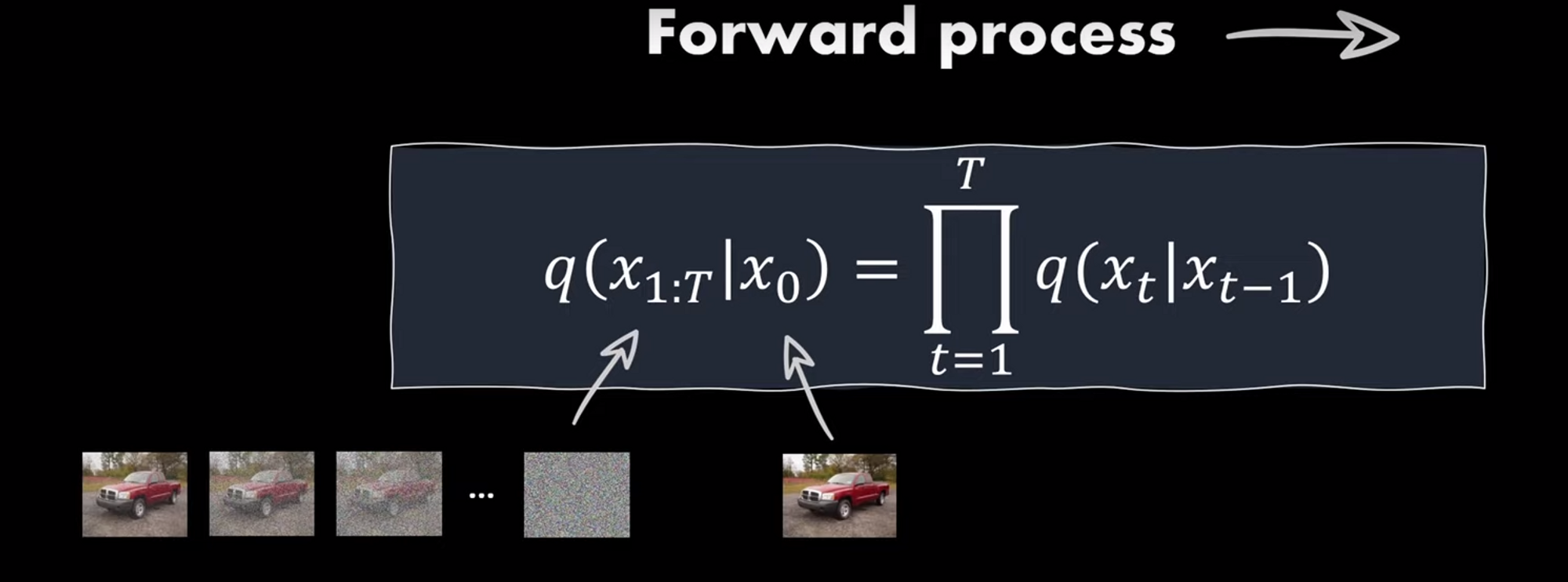
x0 는 항상 초기 입력 값이고 다른 x1:T 값은 노이즈가 많은 버전입니다.

 

노이즈가 샘플링 되는 방식은 아래와 같습니다.

• 베타 시퀀스는 variance schedule입니다. variance schedule은 각 시작 단계에서 얼마나 많은 양의 noise를 추가할지 정해줍니다.
• xt-1은 noise가 적은 이전 이미지입니다.
• 매 step마다 gaussian distribution에서 reparameterize를 통해 sample하게 되는 형태로 noise는 추가되는데, 이때 단순히 noise만을 더해주는게 아니라 루트 1-베타t 로 scaling하는 이유는 variance가 발산하는 것을 막기 위함입니다.
• variance를 unit하게 가둠으로써 forward-reverse 과정에서 variance가 일정수준으로 유지될 수 있게 된됩니다

 

 

 

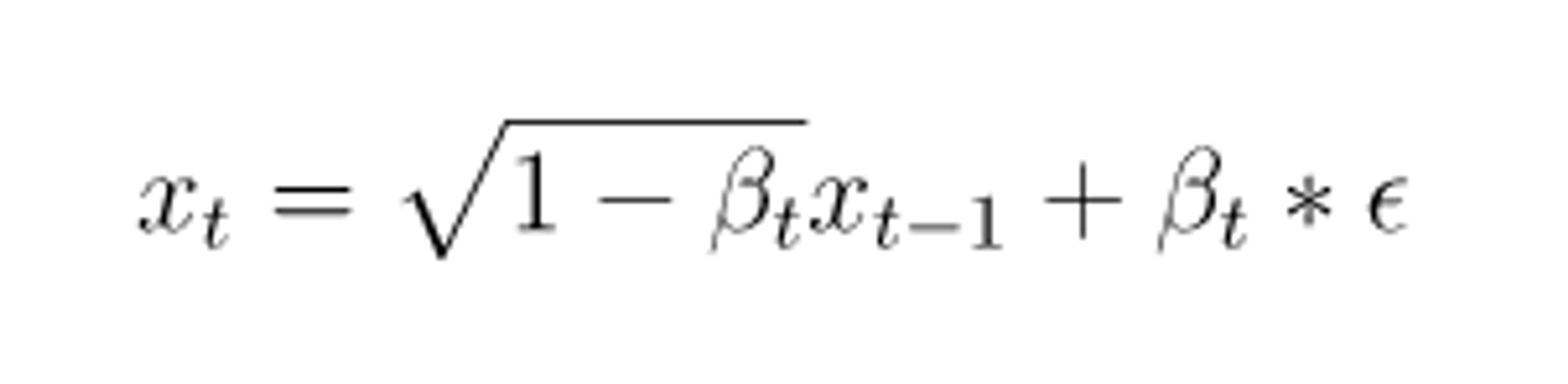
위의 수식을 토대로해서 이미지를 펼치게 되었을 때 t-1의 이미지가 주어졌을 때 t의 이미지의 분포는 아래와 같은 가우시안 분포를 따른다고 합니다. 위의 식은 아래의 그림으로 설명 가능합니다.

 

위의 수식을 토대로 0번째 이미지에서 바로 t번째 이미지 분포를 구할 수 있으며 이 또한 가우시안 분포를 따르며 해당 수식을 통해 나중에 나올 loss값을 구하게 됩니다.

이미지의 각 픽셀에는 빨강 녹색 파랑의 3개의 채널이 있으며 이 값은 일반적으로 0-255 사이의 값을 가지거나 정규화시 -1과 1사이의 값으로 나타납니다.

 

아래의 그림에서 녹색과 파랑의 값을 -1로 지정합니다.

이제 이미지의 분포는 이제 다음과 같은 평균과 분산으로 설명 가능합니다.

 

첫 번째 이미지에서 해당 단일 픽셀에 대한 분포의 평균은 예를 들어 첫 번째 이미지의 경우 0.99가 될 수 있습니다. 큰 베타를 설정하면 분산이 더 잘 고정됩니다.

이는 픽셀 분포가 더 넓을 뿐만 아니라 이 분포에서 샘플링할 때 이미지가 더 손상되어 결과적으로 노이즈가 더 많아집니다. 결국 베타는 표준 가우시안 분포에 해당하는 평균 0으로 수렴하는 속도를 제한합니다.

 

 

중요한 부분은 평균이 0이고 모든 방향에서 픽스된 분산을 갖는 가우시안 분포에 도달하도록 적절한 양의 노이즈를 추가하는 것입니다. 그렇지 않으면 나중에 샘플링이 잘 작동하지 않을 것입니다.

 

앞서 t번의 sampling을 통해 매 step을 차근차근 밟아가면서 x0에서 xt를 만들 수도 있지만, 임의의 time에 대해 노이즈가 있는 버전을 sampling할 수 있습니다.

 

Closed form forward process

 

예를 들어 diffusion process에서 200단계를 선택한다고 가정해봅시다. ( t=200 )

variance schedule은 각 단계에서 추가할 노이즈의 양을 알려줍니다. ( 베타 값 )

 

저자는 1-베타인 a 알파라는 용어를 정의합니다. 베타가 노이즈니 1-베타인 알파는 원본이미지의 보존 정도?라고 생각하면 될 것 같습니다.

이러한 알파의 누적 곱을 계산하여 한 이미지에서 다음 이미지로 바뀔 때 알파위에 라인이있는 새로운 알파가 탄생합니다.

논문에 나온 Linear Schedule

 

베타값을 정할 때, 데이터가 이미지와 비슷할 때는 베타값을 작게 설정 ( 논문에서 10의 -4 제곱 ) 

데이터가 이미지와 멀어질 때는 베타값을 높게 설정합니다. 

임의의 t값에 대한 이미지 Sampling 방법

 

한 step씩 학습을 진행하면 메모리와 resource가 너무 많이 소모된다. 그러나 이런식으로 한번에 만들면 여기서 loss를 구한 후 t에 대한 expectation을 구하는 식으로 학습이 가능하다.

2.2 Reverse Process

저자는 reverse diffusion 과정에서 u-net 사용을 제안합니다.

오토인코더와 유사한 아키텍쳐를 가지고 있으며 image segmentation에서 널리 사용되는 모델입니다.

출력은 입력과 동일한 모양을 갖습니다.

 

입력은 병목 현상에 도달할 때까지 컨볼루션 및 다운샘플링 레이어를 통과한 다음 텐서가 다시 업샘플링되고 더 많은 컨볼루션 레이어들을 통과합니다.

입력 텐서가 더 작아지지만 채널이 추가되어 더 깊은 형태가 됩니다.

그 외에도 일반적으로 레이어 배치 또는 group 정규화 사이의 Residual connection과 같은 구성요소가 있습니다.

모델은 세 가지 색상 채널이 있는 noise가 추가된 이미지를 입력으로 사용하고 분산이 고정되어 있기 때문에 이미지의 noise를 예측합니다.

Hierarachical VAE에서의 decoding과정과 비슷합니다.

 

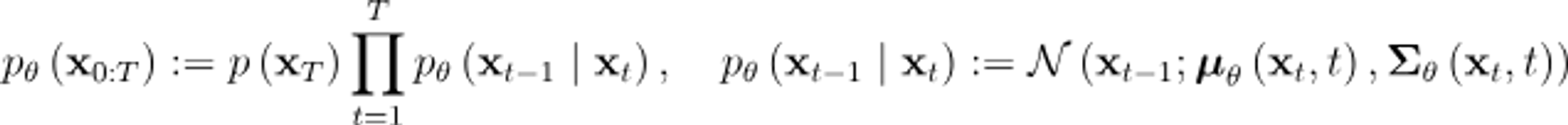
Reverse Process는 제목 그대로 q와는 반대로 noise를 점진적으로 제거하는 denosing process입니다.

그래서 q(xt, xt-1)와는 반대로 time이 뒤바뀐 p(xt-1, xt)로 표현이 됩니다.

즉, Gaussian noise xt에서 denoising 하면서 이미지 x0을 만드는 과정입니다. 

 

정리

 

 

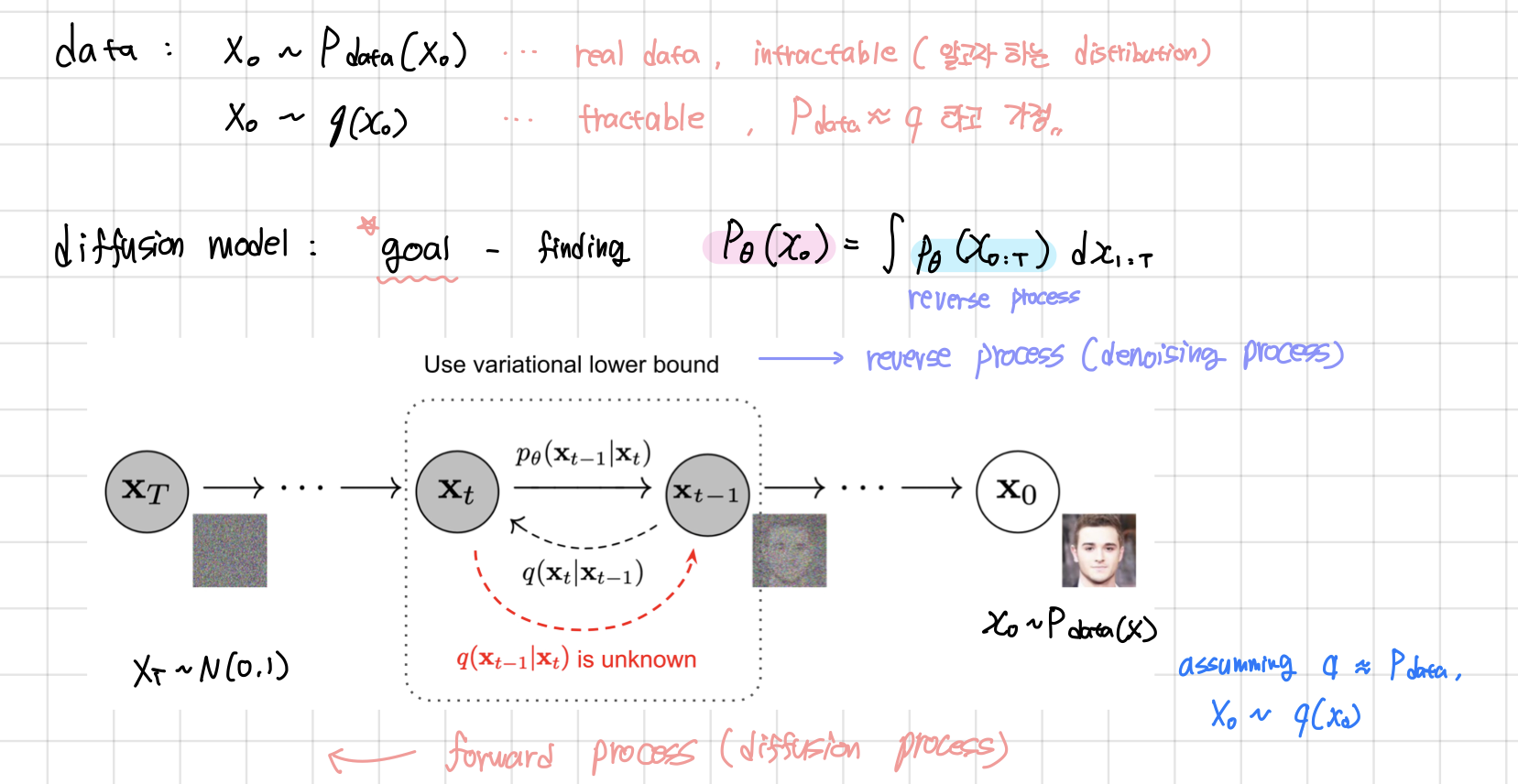
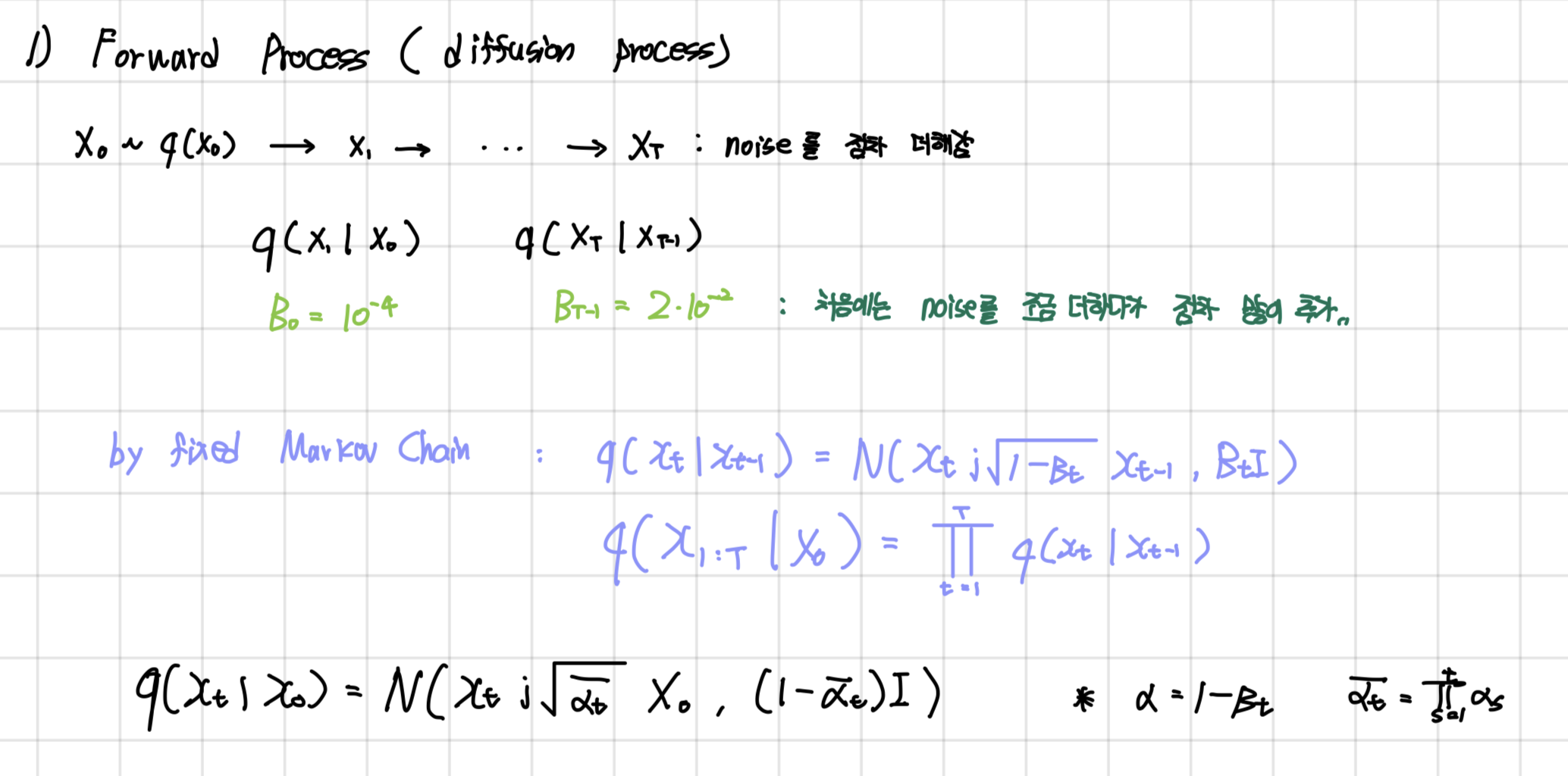
3. Diffusion models and denosing autoencoders 

 

3.1 Objective Function

q(z|x)는 계산이 가능하지만, p(z|x)는 계산이 불가능합니다. 

KL Divergence 값은 항상 0 이상의 양수를 만족하는 성질을 이용하여, (2.8)의 왼쪽식이 Evidence Lower Bound (ELBO)가 되어 ELBO를 최대화는 문제를 풀 수 있습니다. 아래에 다른 기호로 정리된 수식을 보면, (2.8)의 우측식이 사라지고, 좌측식과 유사한 형태가 남은 것을 볼 수 있습니다.

 

 

Lt 부분을 보면 DDPM에서 forward process는 xt가 항상 gaussian distribution을 따르도록 하기 때문에 사실 tractable한 distribution, q(xt | x0 ) 는 prior p(xt)와 거의 유사합니다. 또한, DDPM에서는 forawrd process variance 베타를 constant로 고정시킨 후 approximate posterior를 정의하기 때문에 이 posterior q에는 learnable parameter가 없습니다.  

 

따라서 이 loss term은 항상 0에 가까운 상수이며 학습과정에서 무시됩니다. 

 

Lt-1은 x0부터 시작하여 conditional하게 식을 전개하다보면, tractable한 forward process posterior q(Xt-1 | Xt, X0) 의 정규 분포를 알 수 있는데, 이를 바탕으로 KL divergence 를 계산하면 우리가 결과적으로 학습하고자 하는 p(Xt-1 | Xt)를 학습시킬 수 있습니다.

 

 

algorighm 1 :

데이터 세트에서 일부 이미지를 샘플링한 다음 

t를 샘플링하고 정규 분포에서 노이즈도 샘플링

경사 하강법을 통해 목표로를 최적화합니다. 

 

algorithm 2:

정규분포에서 x t를 먼저 샘플링합니다. xt는 출발점인 데이터입니다.

network를 학습하고 나면 , gaussian noise에서 시작해서 순차적으로 denoising 하는 것이 가능합니다. 

 

4. Experiment

 

 

Reference 

 

https://happy-jihye.github.io/diffusion/diffusion-1/#21-forward-process-diffusion-process

[Paper Review] DDPM: Denoising Diffusion Probabilistic Models 논문 리뷰

 

https://lilianweng.github.io/posts/2021-07-11-diffusion-models/

What are Diffusion Models?