시계열 분석 개요 - time series analysis
시계열분석(time series analysis)은 시간의 흐름에 따라 일정한 간격으로 사건을 관찰하여 기록한 데이터(=시계열 데이터)를 바탕으로 미래의 관측값을 예측(forecasting)하는 분석 기법입니다.
과거의 관측값을 분석하여 이를 모델링하고, 이 예측 모델을 바탕으로 미래의 관측값을 예측하는 것이지요.
시계열 데이터는 일반적으로 추세 성분(trend component), 계절 성분(seasonal component), 불규칙 성분(irregular component) 등으로 구성되며 이 성분들에 의해 변동된다고 가정합니다.
시계열 분석 절차
1. 시계열 데이터 생성
2. 탐색적 분석을 통해 데이터의 특성 이해 -
시각화(visualization) 작업을 통해 시계열 데이터의 변동 패턴 관찰합니다.
성분 분해(component decomposition) 작업을 통해 추세, 계절, 불규칙 성분으로 세분화 합니다.
3. 미래 관측값에 대한 예측 -
지수모델링(exponential modeling) 기법
ARIMA(autoregressive integrated moving average) 기법
시계열 데이터 분해 ( time series data decompose )
시계열 데이터를 추세/계절/불규칙 요소로 분해하는 기법ㅋ
추세 성분 - 시간의 흐름에 따른 수준(level, 즉 관측값의 크기)의 변화
계절 성분 - 단위 기간 내에서의 순환 주기의 영향
불규칙 성분 - 추세 성분과 계절 성분에 의해 설명되지 않는 영향

가법모델 ( additive model ) 과 승법모델( multiplicative model )
- 가법 모델은 변동폭이 일정하지만 승법모델은 변동폭 수준에 비례하여 증폭되므로 승법모델이 보다 적합.
- 승법 모델보다 가법 모델이 시계열 분석에 적합하므로 승법 모델을 가법 모델로 변환하여 사용이 가능. ( 승법 모델에 log를 적용 )

R 프로그래밍은 유튜브에서 곽기영 교수님의 수업으로 독학 중입니다.
R 로 머신 러닝을 하는 강좌가 별로 없는데 곽기영 교수님의 유튜브에 정말 정리가 잘 되어 있어서 도움을 많이 받았습니다.
위에 제가 정리한 부분을 보시면
시계열 데이터를 분해한다는 것은 앞서 말씀드렸듯이 추세, 계절, 불규칙 성분으로 나눠서 보는 것입니다.
co2 <- window(co2, start=c(1985,1), end=c(1996,12)) 를 통해 데이터를 가공하겠습니다.
이는 1985년 1월부터 1996년 12월까지 co2 의 데이터를 추출하는 겁니다.
그 다음으로 stl() 함수를 통해서 데이터 분해를 할 수 있습니다.
첫 번째 인자로 데이터를 지정하고 , 그 다음으로 s.window 매서드에는 기간을 설정할 수 있습니다. 가령 'periodic'은 전범위를 기간으로 설정하는 것입니다.
계절 요인 분해와 비계절적 요인 분해
계절적 요인을 제거한 데이터를 보고 싶다면 이런 식으로 코드를 작성하시면 됩니다.
co2.decomp
# 계절 효과가 제외된 시계열 데이터
plot(co2.adj, col="tomato", lwd=2,
xlab="Year", ylab="CO2 Concentration (parts per Million)",
main="CO2 Concentration Time Series without seasonal effect")

ma() 함수를 통해서 비계절 데이터를 분해할 수 있습니다.
ma 함수는 'forecast' 라이브러리에 포함되어 있습니다.
ma() 첫 번째 인자로 시계열 데이터 값, 두 번째 인수로 관측값 개수(k)를 입력하시면 이동평균값을 계산합니다.
k 값이 클수록 데이터의 시계열 패턴을 명확하게 관찰이 가능하죠.
정상성과 자기상관
우리는 왜 계절적 요인과 비계절적 요인을 제거하는 과정을 거쳐야 할까요?
이는 시계열 데이터 분석에 꼭 필요한 성질인 정상성 때문입니다.
시계열 분석에서 가장 널리 사용되는 ARIMA 예측 모델은 시계열 데이터의 정상성(stationarity)을 가정합니다.
정상성이란 시계열 데이터의 특성이 시간의 흐름에 따라 변하지 않는다는 것을 의미해요.
정상이 normal 을 뜻하는 것이 아니라 stay 로 이해하는 것이 편합니다.
정상성이 있는 시계열, 즉 정상 시계열은 장기적으로 예측 가능한 패턴을 갖지 않으며, 시계열 그래프는 일정한 변동폭( 즉 일정한 분산 )을 가지면서 대체로 수평에 가까운 패턴( 즉 일정한 평균 )을 보입니다.
데이터가 정상성을 가진다는 것은 평균과 분산이 안정화되어 있어서 분석하기 쉽다는 것을 의미하죠.
그렇기 때문에 추세나 계절요인은 시간이 경과하면서 관측값에 영향을 미치기 때문에 추세 성분이나 계절 성분을 갖는 시계열은
비정상적(non-stationary)라고 합니다.
불규칙 성분만으로 구성된 시계열은 정상적( 어느 시점에서 관찰하든 관측값은 불규칙한 변동을 제외하면 동일한 모습을 가짐 )입니다.
따라서 추세나 계절적 요인이 포함되어 있어서 데이터가 정상성을 갖지 않으면 그러한 복잡한 패턴을 모델링하여 분석하는 것이 어렵기 대문에 일반적으로 정상성을 갖도록 전처리를 수행합니다.
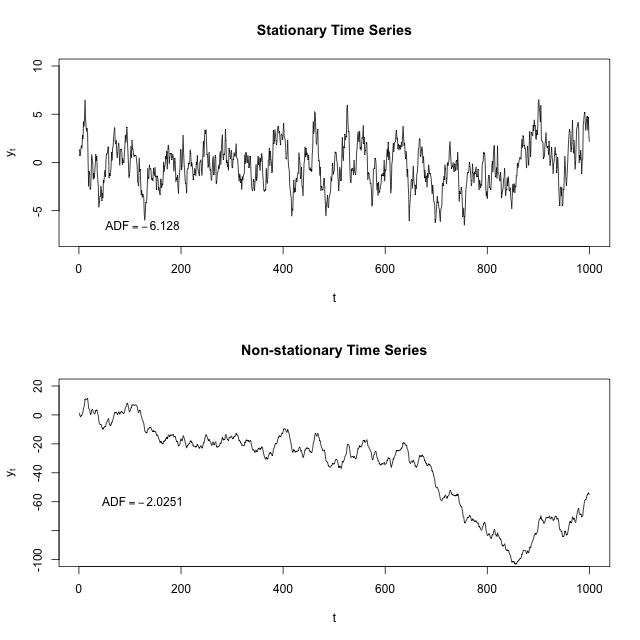
아래에 있는 그래프를 보시면 밑으로 하락하는 추세를 관찰하실 수 있습니다.
전처리 과정에서 추세를 제거한 시계열 데이터로 만드는 과정이 필요해 보이네요.
자기상관
정상 시계열은 어느 시계열 구간에서 관찰하든 평균과 분산이 일정하며, 또한 관측값 간의 공분산도 일정합니다.
이는 자기상관(autocorrelation)이 시간에 따라 변화하지 않는다는 것을 의미합니다.
자기상관은 동일한 변수를 시점을 달리하여 관찰하였을 때, 이 관측값들 사이의 상호 관련된 정도를 나타내는 척도라고 할 수 있죠.
자기 상관은 다른 시점의 관측값 간 상호 연관성을 나타내므로 이는 시차를 적용한 시계열 데이터 간의 상관관계를 의미합니다.
그림을 보면 이해가 더 잘 될거 같습니다.

시차에 따른 일련의 자기 상관을 자기상관함수(autocorrelation function, ACF)라고 합니다.
ACF는 시차에 따른 관측값 간의 연관 정도를 보여주며, 시차가 커질수록 ACF는 점차 0에 가까워지게 됩니다.
정상 시계열의 경우 ACF는 상대적으로 바르게 0으로 접근하고
비정상 시계열의 ACF는 천천히 감소하여 종종 큰 양의 값을 가지게 되요.
편자기상관함수
편자기상관(partial autocorrealation)은 시차가 다른 두 시계열 데이터 간의 순수한 상호 연관성을 나타냅니다.
편자기상관 PACk 는 원래의 시계열 데이터 Yt 와 시차 k 시계열 데이터 Yt-k 간의 순수한 상관관계로서 두 시점 사이에 포함된 모든 시계열 데이터의 영향은 제거됩니다.
시차에 따른 일련의 편자기 상관을 편자기상관함수(PACF)라고 합니다.
ACF 와 PACF in R
R에서 ACF 와 PACF를 plot 해보겠습니다. 이는 시계열 데이터의 정상성을 평가하고 ARIMA 모델의 패러미터 결정 및 모델의 적합도를 평가하는 것에 활용됩니다.

다음은 fpp2 패키지에 포함된 goog200 ( 200일간의 구글 주가 ) 에 대한 ACF 도표입니다.
Acf(goog200,main = "Google stock Prices" )
R에서는 이렇게 간단한 함수로 Acf 함수를 호출하고 사용할 수 있습니다.
도표를 보시면 파란색 점선으로 표시된 부분은 자기 상관 0에 대한 95% 신뢰구간을 표시한 것입니다.
그렇다면 위의 도표는 모든 차수에서 자기 상관이 95% 를 벗어난다는 점을 확인할 수 있고
이는 0이 아닌 자기 상관이 드러나며 비정상 시계열 데이터임을 알 수 있습니다.
데이터를 가공한 후 ( 차분 ) 의 그래프를 보실까요?

Acf(dgoog200,main = "Google stock Prices Transformed by Differencing" )
데이터를 차분하는 과정을 통해 수정된 데이터 dgoog200 을 확인해본 결과 모든 차수에서
자기상관 0에 대해 95% 신뢰구간을 만족하는 것을 확인하실 수 있습니다.
다음 포스팅에서는
시계열 데이터 분석의 처음 ( 데이터 불러오기, 전처리 ) 부터 마지막 검정 ( adf 검정 ) 까지 R로 실습해보겠습니다.
감사합니다

