
SSM(Space State Model)은 뭐야 ?
SSM은 기존 Transformer(https://minyoungxi.tistory.com/104) 기반 모델에 비해 다양한 작업에서 계산 비용이 낮으면서 큰 잠재력을 보이며 주목받고 있습니다. 제어 이론 및 계산 신경 과학에 뿌리를 두고 있으며, 동적 시스템을 상태 변수로 모델링하여 딥러닝에 적용됩니다.
그렇다면 Transformer의 문제는 무엇일까요 ?
Transormer는 Attention 기법을 통해서 일반적으로 장거리 종속성을 개선했지만, Transformer의 문제점은 유전체 또는 극도로 긴 텍스트와 같은 맥락에서는 확장이 잘 되지 않습니다.

왜 극도로 긴 input에서 느릴까 ? self-attention 매커니즘 때문. self-attention은 입력 시퀀스의 모든 토큰 쌍 사이의 상호작용을 계산해야 합니다. 이는 시퀀스의 길이가 $n$ 일 때, $O(n^2)$ 의 시간 복잡도를 가지며, 메모리 사용량도 동일하게 $O(n^2)$ 로 증가합니다. 따라서 입력 시퀀스가 길어질수록 연산량과 메모리 사용량이 기하급수적으로 증가합니다.
SSM은 최근 크게 주목받고 있는 Mamba 알고리즘의 self-attention과 같다고 볼 수 있습니다.
1차원 input을 입력받아서 잠재 공간에 매핑 후 다시 1차원 출력으로 내보내는 것입니다.

SSM은 긴 시퀀스를 효율적으로 모델링할 수 있으며, Transformer와 달리 메모리와 계산 자원을 덜 소모합니다.
위의 수식을 보면 선형적인 계산 복잡도를 가지고 있으며 , 효율적인 훈련을 위한 병렬적 계산이 가능합니다.
하지만 더 많은 메모리가 필요할 수 있으며 훈련 중에 그래디언트 소실 문제가 발생할 수도 있습니다.
Deep SSM
아래에 나타난 상태공간 방정식은 1차원 입력 신호를 N 차원의 잠재 상태 $x(t)$ 로 mapping 한 후에 1차원 출력 신호 $y(t)$ 로 투영합니다. 즉, 입력 신호인 $u(t)$를 state representation vector $x(t)$ 와 출력 벡터 $y(t)$로 매핑하는 것이죠.
$\acute{x}(t) = A(t)x(t) + B(t)u(t)$ -> 시간에 따른 $x(t)$의 변화량
$y(t) = C(t)x(t) + D(t)u(t)$
$x(t) \in \mathbb{R}^n$, $y(t) \in \mathbb{R}^q$, $u(t) \in \mathbb{R}^p$ 는 각각 상태 벡터, 출력 벡터, 입력 (또는 제어) 벡터를 나타냅니다.
$\dot{X}(t) = \frac{d}{dt} X(t)$
$A(t) \in \mathbb{R}^{n \times n}$,
$B(t) \in \mathbb{R}^{n \times p}$,
$C(t) \in \mathbb{R}^{q \times n}$, 그리고 $D(t) \in \mathbb{R}^{q \times p}$ 는 각각 상태 행렬, 입력 행렬, 출력 행렬, 피드포워드 행렬을 나타냅니다.
시스템 모델에 직접적인 전달 경로가 없을 때, $D(t)$는 영 행렬이 되며, 따라서 다음과 같은 단순화된 방정식을 얻을 수 있습니다:
$$
\dot{X}(t) = A(t)X(t) + B(t)U(t)
$$
$$
y(t) = C(t)X(t)
$$
시스템이 연속적이므로 컴퓨터에 입력하기 전에 이를 이산화(Discretion)해야 합니다. Mamba 아키텍처에서는 영차 유지(Zero-Order Hold, ZOH) 방식을 채택하여 이산화합니다:
$$
X_t = \bar{A} X_{t-1} + \bar{B} U_t
$$
$$
y_t = C X_t
$$
여기서
$\bar{A} = \exp(\Delta A)$,
$\bar{B} = (\Delta A)^{-1}(\exp(\Delta A) - I) \cdot \Delta B$,
$\Delta$ 는 스텝 크기를 나타냅니다.
연속함수 $u(t)$ 대신 이산 입력 시퀀스 ($u_1$ , $u_2$, ... )에 적용하기 위해 SSM은 입력의 해상도를 나타내는 step size로 이산화되어야 합니다.
만약 $state$ $vector$와 $input$ $vector$를 $h$와 $x$를 사용하여 나타내고 싶다면 아래의 함수를 통해 RNN의 방식과 유사한 연산으로 나타낼 수 있습니다.
function to function 이 아닌 sequence to sequence mapping 으로 바뀌게 되고, 상태 방정식이 $x_k$ 의 재귀적 표현이 되어 discrete SSM을 RNN처럼 계산할 수 있게 됩니다.
$h_t = \bar{A}_t-1 + \bar{B}x_t$
$y_t = Ch_t$
그러나 RNN 모델은 계산할 때 병렬화(parallelized)할 수 없는 문제에 직면합니다. 위의 수식을 단순히 확장하면 다음과 같습니다.
$$ y_0 = C \bar{A}^0 \bar{B}x_0 $$ $$ y_1 = C \bar{A}^1 \bar{B}x_0 + C \bar{A}^0 \bar{B}x_1 $$ $$ y_2 = C \bar{A}^2 \bar{B}x_0 + C \bar{A}^1 \bar{B}x_1 + C \bar{A}^0 \bar{B}x_2 $$
마지막 항과 끝에서 두 번째 항의 곱셈자는 항상 $C \bar{A}^0 \bar{B}$ 및 $C \bar{A}^1 \bar{B}$입니다. 따라서 우리는 이 곱셈자들을 컨볼루션 커널로 취급할 수 있습니다:
$$ \bar{K} = C \bar{B} \cdot (\bar{A}^0, \bar{A}^1, \bar{A}^2, \ldots, \bar{A}^L) $$
여기서 $L$은 주어진 입력 시퀀스의 길이입니다. 우리는 식 (4)를 다음과 같은 컨볼루션 형식으로 다시 쓸 수 있습니다:
$$ \bar{K} = (CB, CAB, \ldots, CA^kB, \ldots) $$ $$ y = x \ast \bar{K} $$
이렇게 하면, 우리는 병렬 학습과 선형 복잡도의 반복 형식 추론에 적합한 완전한 SSM 모델을 얻을 수 있게 됩니다. Transformer 아키텍처에서는 문맥 정보가 유사도 행렬에 저장되지만, SSM은 유사한 모듈이 없어 문맥 학습 성능이 떨어집니다.
위의 수식을 통해 SSM 모델의 계산 복잡도가 입력 시퀀스의 길이에 선형적으로 비례한다는 것을 확인할 수 있음. 따라서 이 모델은 입력 시퀀스의 길이에 따라 선형 복잡도를 가짐. 이와 같은 선형 복잡도를 통해 SSM 모델은 병렬 학습과 효율적인 추론을 실현할 수 있음.
Transformer 모델에서 주로 사용되는 self-attention의 계산 복잡도는 $O(n^2d)$ 입니다. $n$은 시퀀스의 길이 , $d$는 임베딩 차원입니다. 즉, 시퀀스의 길이에 대해 제곱에 비례하여 계산 복잡도가 증가하는 것이죠.
반면, SSM 모델의 계산 복잡도는 $O(nd)$ 이므로 시퀀스의 길이에 대해 선형적으로 계산 복잡도가 증가합니다.
SSM의 다양한 변형이 존재하며, 이들은 특정 응용 분야에 맞게 최적화되었습니다. 예를 들어, Kalman 필터는 상태 공간 모델의 대표적인 변형 중 하나로, 잡음이 포함된 시스템의 상태를 추정하는 데 사용됩니다. 또한, 확장된 Kalman 필터(Extended Kalman Filter, EKF)와 무향 Kalman 필터(Unscented Kalman Filter, UKF)와 같은 비선형 변형도 존재합니다.
최근에는 SSM의 개념을 딥러닝 모델에 통합하려는 시도가 이어지고 있습니다. 특히, SSM은 긴 시퀀스 데이터를 처리하는 데 있어 계산 복잡도를 낮추는 데 강점을 보입니다. 이러한 이유로 SSM은 Transformer 모델의 대안으로 주목받고 있으며, 다양한 연구자들이 이를 개선하고 최적화하려는 노력을 기울이고 있습니다.
HiPPO
HiPPO는 SSM 논문들 중 가장 흥미롭게 읽은 논문입니다. HiPPO 이전에 Parallelizing Legendre Memory Unit Training(LMU)
라는 논문이 있는데요, 해당 논문에서는 RNN의 단점 중 하나인 병렬화 불가능 문제를 linear recurrence convolution으로 해결하는 시도를 했습니다.
만약 우리가 특정 input의 이전/이후 state를 가져올 수 있는 딜레이 구조의 시스템을 구축할 수 있다면, 해당 시스템의 output으로 input의 recurrence 구조를 확보할 수 있다는 장점이 생깁니다. 우리는 Linear system을 찾고자 하기 때문에 (애초에 학습하고자 하는 신경망 연산 자체가 텐서 및 행렬 기반이기 때문이라 생각하면 편합니다), 다음과 같이 네 개의 matrices 로 표현되는 LTI system을 찾는 것이 목표가 됩니다.
요약하자면, 이상적인 딜레이 시스템을 LTI 시스템으로 구축하여 표현한 것이 기존의 Linear State Machine 디자인이었고, 이를 다시 non-linear neural network system을 사용하여 학습한 것이 LMU 구조입니다.
HiPPO는 polynomial bases에 projection을 해서 continuous-signal과 discrete-signal을 online하게 compression 합니다. HiPPO 모델을 요약하자면, 고차 다항식 프로젝션 연산자를 사용하여 시퀀스 데이터의 정보를 압축하고 모델의 효율성을 높이는 알고리즘입니다.
> HiPPO model combines the concepts of Recurrent Memory and Optimal Polynomial Projections, which can significantly improve the performance of recursive memory, This mechanism is very helpful for SSM to handle long sequences and long-term dependencies.
HiPPO 논문을 보시게 되면 정말 많은 수식들을 볼 수 있습니다.
각 time step의 중요도 measurement가 정의되면, HiPPO는 "natural online function approximation problem"의 optional solution을 찾아냅니다. 아래의 그림처럼 $f(t)$라는 ground truth input이 주어졌을 때, 정보의 손실을 최소화하는 방향으로 $g(t)$를 얻어낼 수 있습니다. 이때, $g(t)$는 orthogonal polynomials(OP)를 활용해서 구할 수 있습니다.
모든 시간 $t$ 에는 $f$를 polynomial-space로 optimal projection 하는 $g(t)$가 있는 것이죠. 아래의의 예시에서는 orthogonal polynomial basis(OP basis)가 4개입니다. 각각의 coefficient $c(t)$는 해당 시점에서 OP basis에 사영(projection)된 값을 나타냅니다.
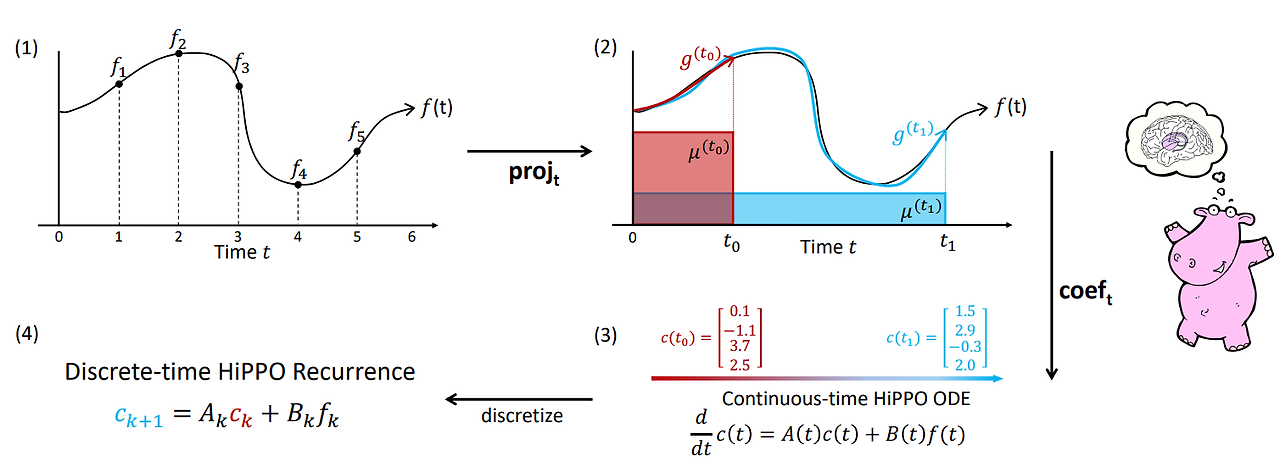
$C(t)$는 HiPPO에서 모든 시간 t에 대해 0~$t$ 시간에 대한 정보의 총합으로 볼 수 있는 $C_t$ 를 유지하기 위한 프레임워크 입니다. 적절한 bias를 선택함으로써 $C(t)$ 는 history를 나타내게 됩니다. ( $C_t$ 와 $t$ 시점의 출력 $f_t$ 의 선형 조합을 통해 $C_t+1$ 을 생성합니다.)
HiPPO를 행렬 형태로 구현하여 SSM에 적용하면 SSM의 성능을 크게 향상시킬 수 있습니다.
이전 연구의 문제는 SSM이 실제로 성능이 매우 낮다는 것이었죠.
- Sequence의 길이에 따라서 기울기(gradient)가 기하급수적으로 증가/감소하는 문제가 발생했습니다.
- Discrete-time SSM을 보면 이산 시간 간격 $\Delta$ 에 대한 $A$를 $\bar A$ 로 표기한다는 것이죠. Continuous-time 에서는 현재 상태 $x(t)$ 를 사용하여 $y$를 계산하고, Discrete-time 에서는 업데이트한 후에 업데이트 된 $x$ 를 사용하여 $y$를 계산합니다.
Summary
HiPPO(High-order Polynomial Projection Operator) 방법은 연속 함수 $f$를 Hilbert 공간 $u$에서 예측 함수 $g$의 서브스페이스로 변환하여 이를 적절한 벡터 기반의 계수 배열로 표현하는 방법입니다. 이를 통해 연속 시간 미분 방적식을 LTI(선형 시불변) 시스템의 미분 방정식으로 변환할 수 있습니다. 이 과정에서 시스템의 주축이 되는 함수 $A(t)$와 $B(t)$의 형태를 결정하여 시퀀스 메모리의 중요도를 매핑합니다.
기존의 LMU(LeGendre Memory Unit)는 특정 슬라이딩 윈도우 크기 $\theta$ 를 가지는 이상적인 딜레이 시스템의 LTI 미분 방정식을 이산화하여 사용하지만, HiPPO는 이를 연속 시간 메모리화로 일반화한 것입니다.
S4
S4 모델은 이러한 제한을 해결하기 위해 구축되었습니다.
Method: Structured State Spaces (S4)
Efficiently Modeling Long Sequences with Structured State Spaces
LSSL은 state space model (SSM) 을 Simulating 하느라 느리고 memory도 많이 차지한다고 합니다. 이를 해결하기 위해 S4 모델을 제안합니다.
LSSL은 선형 상태 공간 모델로, 시간 시계열 데이터나 연속된 데이터의 학습 및 예측에 많이 사용됩니다. LSSL의 주요 문제점은 다음과 같습니다:
• 느린 계산 속도: 상태 공간 모델은 일반적으로 연산 복잡도가 높아 학습과 예측 과정에서 시간이 많이 소요됩니다.
• 높은 메모리 사용: 상태 공간 모델은 많은 파라미터를 다루어야 하므로 메모리 사용량이 많습니다.
LSSL 에서는 state matrix A를 구하기 위해 L 개의 successive multiplication (연속 곱셈)을 수행해야 하는데, 이는 계산 복잡도가 높아져 Bottle neck 현상을 일으킵니다. -> A를 여러번 곱하는 과정은 시간 복잡도가 $O(L)$ 로, L이 커질수록 계산이 매우 느려집니다.
LSSL의 문제를 해결하기 위해 A를 canonical form으로 변환하면 계산 효율성을 크게 향상시킬 수 있습니다. A를 대각행렬(diagonal matrix)으로 만들면, 행렬 곱셈이 대각 원소들 간의 곱셈으로 단순화되어 계산이 훨씬 빠르고 tractable 합니다.
S4는 A matrix에 low-rank correction (stably diagonalized)를 적용하고, cauchy kernel을 이용해서 SSM computation을 낮춥니다. Path-X 문제를 풀어냈고, LRA에서 SOTA를 달성하게 됩니다.
> 대각 행렬을 이용하면 계산이 훨씬 단순하고 효율적입니다. 하지만 일반 행렬을 대각화하는 것은 쉽지 않죠. 실제로는 다양한 수학적 기법과 최적화가 필요합니다. S4 모델에서는 이러한 문제를 해결하기 위해 low-rank correlation과 같은 기법을 사용하여 계산 효율성을 높입니다.
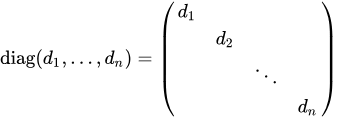
논문에는 수식이 너무 많습니다. 어쨌든 HiPPO matrices (A matrix in SSM) 들을 diagonalize 하는 데 성공했고, 이를 이용해서 굉장히 빠른 속도, 성능을 낼 수 있다는 것입니다.
아래의 결과를 보면 확실히 LSSL에 비해 학습 단계에서 소요 시간과 메모리 할당량 모두에서 훨씬 효율적인 것을 알 수 있습니다. 특히, 차원이 커질수록 S4의 효율성이 더욱 두드러지게 나타납니다. 512 차원에서 S4는 학습 시간이 29.6배 더 빠르고, 메모리 사용량은 392배 더 적네요.
또한 Transformer 모델 대비 입력 시퀀스 길이 1024에서는 1.58배 더 빠르며, 길이 4096에서는 5.19배 더 빠릅니다.
결론적으로 S4 모델은 Transformer 모델에 비해 큰 시퀀스 길이에서 훨씬 더 빠르고 메모리 효율적입니다. 특히, 길이가 길어질수록 S4의 효율성이 두드러집니다. 이는 S4 모델이 실제 대규모 시퀀스 데이터를 처리하는 데 매우 유리할 것 같습니다.

Review
모든 딥러닝 모델들에는 수많은 수식이 있지만, 특히 이번에 리뷰할 때 주로 읽었던 State Space Model for New-Generation Network Alternative to Transformers: A Survey : https://arxiv.org/abs/2404.09516
논문과 각각의 개별 논문들 ( HiPPO, LSSL 등 ) 은 특히 너무 많은 수식으로 인해 어려움을 많이 겪었습니다.
Continuous time memorization 에 대한 근사화(approximation)는 HiPPO 그리고 LSSL 논문에서 공통적으로 가지는 이론적/기술적 배경에 해당됩니다. 다음 논문 리뷰에서는 연속 시간 모델링을 이산 시간 모델로 근사화 혹은 다운 샘플링하는 과정에 대해서 깊게 이해해볼까 합니다. Mamba에서는 ZOH 방법을 사용한다고만 간단하게 나와있는데, SSM의 발전 과정과 앞으로의 논문 이해를 위해 한 번 짚어보고 가야할 것 같네요 !
